Решение типовых задач

1. В ящике находятся три белых и два черных шара. Из ящика вынимается наудачу один шар. Найти вероятность того, что этот шар будет белым.

Решение. Событие, состоящее в появлении белого шара, обозначим через А.

Общее число случаев .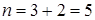

Число случаев, благоприятствующих событию А, .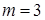

Тогда: .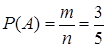

2. В урне находится 10 белых и 6 черных шаров. Из урны наудачу вынимаются два шара. Найти вероятность того, что оба шара будут белыми.

Решение. Обозначим через А событие, состоящее в появлении двух белых шаров.

Общее число возможных случаев

.

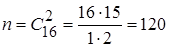Число случаев, благоприятствующих событию А

.

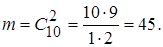
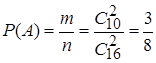3. В партии из 10 деталей 7 стандартных. Найдите вероятность того, что среди шести наудачу взятых деталей 4 стандартных.

Решение. Общее число возможных исходов 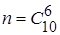. Подсчитаем число исходов, благоприятствующих интересующему нас событию: четыре стандартные детали можно взять из семи стандартных деталей 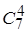способами; при этом остальные 6-4=2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10-7=3 нестандартных деталей можно 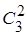способами.

Следовательно, число благоприятствующих исходов равно

.

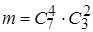Искомая вероятность равна

.

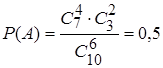4. Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,75, вторым стрелком – 0,8, третьим стрелком – 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель.

Решение. .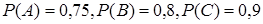

События А,В,С – независимые.

Применяем теорему умножения вероятностей:

.

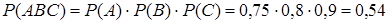5. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один стрелок.

Решение. Вероятность того, что в мишень попадет первый стрелок и не попадет второй, равна

.

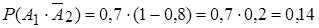Вероятность того, что попадет второй стрелок в мишень и не попадет первым равна:

.

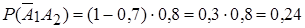Вероятность того, что в мишень попадет только один стрелок, равна сумме этих вероятностей:

.

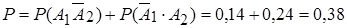6. Устройство содержит три независимо работающих элемента. Вероятности отказа элементов соответственно равны: 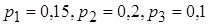. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.

Решение.

;

;

;

.

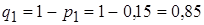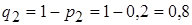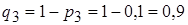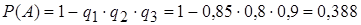7. Для некоторой местности среднее число ясных дней в июле равно 25. Найти вероятность того, что первые два дня июля будут ясными.

Решение.

Событие А – был солнечный день 1-ого июля;

Событие В – был солнечный день 2-ого июля.

При этом события А и В зависимы.

.

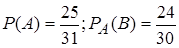По теореме умножения вероятностей зависимых событий получаем

.

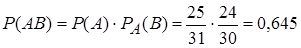8. На предприятии работают две бригады рабочих: первая производит в среднем 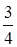продукции с процентом брака 4%, вторая - 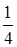продукции с процентом брака 6%. Найти вероятность того, что взятое наугад изделие:

а) окажется бракованным;

б) изготовлено второй бригадой при условии, что изделие оказалось бракованным.

Решение.

а) Событие А – взятое наудачу изделие бракованное. Рассмотрим две гипотезы:

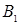- изделие изготовлено первой бригадой;

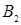- изделие изготовлено второй бригадой.

; .

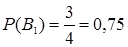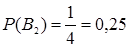Условные вероятности события А соответственно равны:

; .

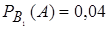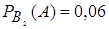Искомую вероятность 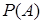найдем по формуле полной вероятности:

.

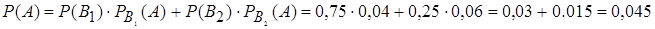б) Для определения вероятности того, что бракованное изделие изготовлено второй бригадой, воспользуемся формулой Байеса:

.

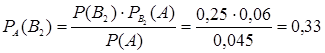Дата добавления: 2015-09-02