Читайте также:
|
В процессе перехода от приведенной формы модели к структурной возникает проблема идентификации. Поэтому структурные модели можно подразделить на: идентифицируемые, неидентифицируемые и сверхидентифицируемые.
Если обозначить число эндогенных переменных в j -м уравнении системы через Н, а число экзогенных переменных, которые содержаться в системе, но не входят в данное уравнение, - через D, то условие идентифицируемости: D+1=H – уравнение идентифицируемо, D+1<H – уравнение неидентифицируемо, D+1>H – уравнение сверхидентифицируемо. Модель идентифицируема, если каждое уравнение идентифицируемо. Если хотя бы одно из уравнений неидентифицируемо, то вся модель неидентифицируема. Система сверхидентифицируемой, если хотя бы одно сверхидентифицируемое уравнение.
Косвенный МНК. Рассмотрим приведенную форму системы 
, в которой 
переменные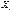 
-не мультиколлинеарны. роцедура статистического оценивания структурных параметров i-го уравнения: На 1-м этапе оцениваем с помощью обычного МНК все параметры 
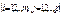приведенной формы. На 2-м этапе используются соотношения 
связывающие структурные параметры i-го уравнения системы с параметрами приведенной формы. В случае точной идентифицируемости i-го уравнения структурной формы его параметры 
и 
однозначно определяются из системы по значениям 
. Подставив в эти соотношения вместо их оценки 
и решив систему уравнений относительно 
и 
, мы получим состоятельные оценки 
и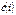 
структурных параметров i-го уравнения системы.
В случае неидентифицируемости анализируемого уравнения структурной формы число взаимно независимых связей между 
, 
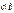и будет меньше общего числа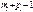 
неизвестных. Поэтому без дополнительной информации нельзя определить значения структурных коэффициентов 
и .
Дата добавления: 2015-09-05; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проблема идентифицируемости СОУ | | | Двухшаговый метод наименьших квадратов. |