Читайте также:
|
Для решения системы 
обычным методом наименьших квадратов препятствует коррелированность значений объясняющей переменной. Для решения этой задачи предполагается следующая процедура На 1-м этапе, чтобы избавиться от 
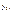в правой части второго уравнения системы, мы заменяем эту переменную ее аппроксимацией с помощью обычного метода наименьших квадратов, который, с учетом центрированности обеих переменных, дает: 
, где МНК-оценка параметров 
парной регрессии 
по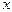 
, как известно, имеет вид 
, а остатки 
в соответствии со свойствами МНК не коррелированы с предиктором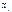 
.
Заменим переменную 
ее аппроксимацией 
.В этом уравнении можно использовать обычный МНК для оценки параметра 
: 
.
Т.о. получаем линейное соотношение, связывающее между собой оцениваемые параметры 
и 
: 
. Для того, чтобы отсюда извлечь оценки 
и 
надо вернуться к соотношениям: 
Решая эти три уравнения относительно параметров структурной формы 
, 
и и воспользовавшись значениями уже подсчитанных оценок 
получаем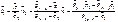 
Дата добавления: 2015-09-05; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проблемы индетификации. Косвенный метод наименьших квадратов | | | ЧЕРЕЗ СТРУКТУРУ СОБСТВЕННОГО СОЗНАНИЯ |