ЗАКЛЮЧЕНИЕ. В данной курсовой работе был проведен анализ устойчивости заданной САР

В данной курсовой работе был проведен анализ устойчивости заданной САР. Выведено дифференциальное уравнение выходного звена. Построены структурная и преобразованная схемы САР. По схемам были определены передаточные функции замкнутой и разомкнутой системы, записаны собственные операторы разомкнутой и замкнутой САР. Определены коэффициенты операторов.

В ходе работы была исследована устойчивость системы. Анализ устойчивости проводился путем построения D-разбиения в плоскости коэффициента усиления 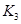. В результате построения были получены три области, одна из которых является областью устойчивой работы САР.

Устойчивость системы в области 1 проверялась при помощи критерия Рауса-Гурвица. Проанализировав знаки a₀ и диагональных миноров, был сделан вывод, что САР является устойчивой в области 1.

Проведена оценка качества регулирования САР по критерию Рауса-Гурвица и Найквиста (рисунок 4), записана таблица с показателями качества регулирования и построены графики выходного сигнала от времени, для коэффициентов .

Проведенный анализ регулирования показал, что при увеличении коэффициента 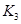качество перерегулирования ухудшается, следовательно, регулятор работает лучше при коэффициенте .

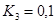Дата добавления: 2015-09-05