|
Читайте также: |
Графически определяем устойчивость системы по АФЧХ (рис.7):
n1=[0.2]; d1=[3.6 1];
n2=[1.6]; d2=[2.8 1];
n3=[2.3]; d3=[1.1 1];
[num1,den1]= series(n1,d1,n2,d2);
[num2,den2]= series(num1,den1,n3,d3);
[num3,den3]= pade(0.6,1);
[num4,den4]= series(num2,den2,num3,den3);
nyquist(num4,den4);
grid on
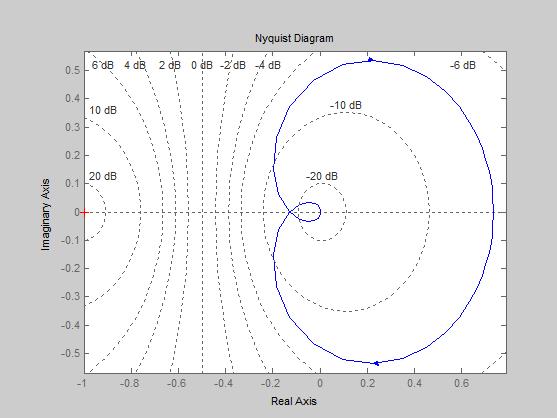
Рисунок7-Частотная характеристика объекта регулирования
На этом графике видно, что система устойчива, так как не охватывает точку (-1,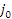 
), так же можно определить запас устойчивости∆А=1-0,12=0,88
Графически определяю устойчивость системы по ЛАФЧХ (рис.8):
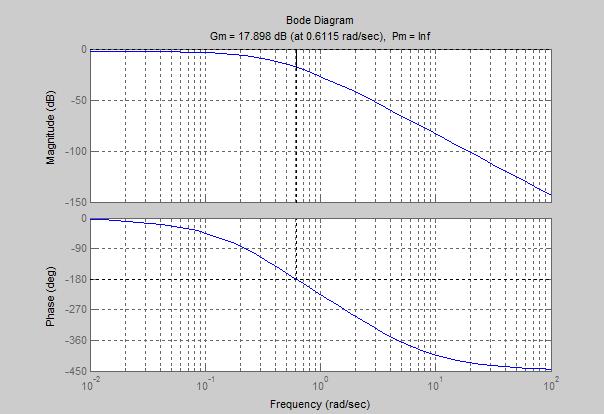
Рисунок 8- Логарифмическая амплитудно-фазовая частотная характеристика
По этому графику можно определить запас устойчивости по фазе и частоте:
Запас по амплитуде: Gm = 17.898 db
Запас по фазе: Pm= inf
Дата добавления: 2015-08-27; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение кривой переходного процесса модели объекта регулирования | | | Выбор закона регулирования и критерия оптимальности процесса регулирования |