Выбор закона регулирования и критерия оптимальности процесса регулирования

В задание мне предлагается использовать ПИ закон регулирования, необходимо проверить может ли этот закон регулирования работать с данным объектом. Для этого нужно рассчитать допустимый динамический коэффициент регулирования, подав на вход единичное ступенчатое воздействие (х_вх=1), найти отношения запаздывания к постоянной времени.

= = 0,18, (6)

Это отношение меньше единицы, значит регулятор непрерывного действия.

Для определения динамического коэффициента я воспользовался графиком(рис. 9):

Рисунок 9 - Динамический коэффициент регулирования на статических объектах (типовой процесс с минимальным квадратичным отклонением, 3 – кривая ПИ регулятор)

Что бы проверить подходит ли регулятор данной системе он должен выполнять следующее условие ,

, (7)

где,

, (8)

следовательно, закон регулирования подходит для данной системы.

Рассчитаем передаточную функцию регулятора с помощью частотных характеристик. Для этого мне необходимо выполнить ряд операций:

Записать передаточную функцию ПИ регулятора:

, (9)

где, = 1,5 с

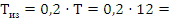2,4 с

Преобразую эту функцию:

, (10)

По графику узнаем допустимое время регулирования

Рисунок 10 – Определение времени регулирования

t_p=16*τ=16*2,2=35,2 сек

Перейдем непосредственно к расчету передаточной функции

Отношение выходной величины системы к входной величине, выраженное в комплексной форме называется комплексной частотной характеристикой (КЧХ) системы.

, (11)

Отношение амплитуд 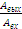является модулем КЧХ, а разность фаз является её фазой.

Для удобства расчетов заменим оператор Лапласа (р) в выражение (5) на jω:

, (12)

Затем избавимся от мнимой единицы в знаменателе, домножим на j числитель и знаменатель

= , (13)

Обозначив в формуле (6) 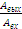= и 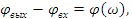получим:

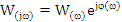, (14)

Зависимость отношения амплитуд выходных и входных колебаний от их частоты называется амплитудно-частотной характеристикой (АЧХ)

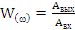, (15)

Амплитудно-частотная характеристика является модулем КЧХ

, (16)

Зависимость разности фазы выходных и входных колебаний от частоты, называется фазочастотной характеристикой (ФЧХ) системы

, (17)

Фазочастотная характеристика является аргументом КЧХ системы.

Дата добавления: 2015-08-27