Основные логические операции и их связки

Математическая логика рассматривает три основные логические операции, а именно: логическое умножение, логическое сложение и логическое отрицание.

Под логическим умножением (связка и) понимают выражение следующего вида:

у = x₁ И х₂ = х₁ /\ х₂ = х₁х₂

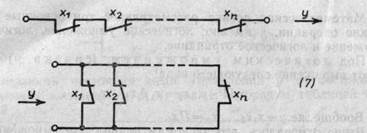
Вообще же у = x₁x₂...x_n = Π x_i.

Выше отмечалось, что аксиомам правил для умножения отвечает зависимость при последовательном включении контактов.

Поэтому логическое умножение моделируется схемой последовательного включения элементов, т. е.

Под л о гически м сложением (связка или) понимают выражение вида

у = х₁ или х₂ = х₁ V x₂ = x ₁ + x ₂· Вообще же

Выше отмечалось, что аксиомам правил для сложения отвечает зависимость при параллельном включении контактов. Поэтому логическое сложение моделируется параллельным включением элементов, т. е.

Под л оги ч еc к и м отрицанием (связка не) понимают зависимость вида

у = НЕх = х.

Вообще же у=x₁x₂... х_п или у=x₁x₂ +... +х_п Черточка над символом обозначает знак отрицания (инверсия).

Выше отмечалось, что обратному значению состояния цепи управления у и сигнала x отвечает цепь с размыкающим

контактом. Поэтому логическое отрицание моделируется цепью с размыкающими контактами.

Пример. Пусть требуется составить цепь управления электролампой у (рис. 10.1, а) от двух выключателей х₁ х₂. Условия включения лампы следующие: при включении х₁ лампа должна загореться, пройдя коридор и воздействуя на х₂, мы лампу выключаем, при обратном движении через кори-

Рис. 10.1. Управление электролампой

дор, воздействуя на х₂, заставляем лампу опять загореться, а воздействуя на х₁, — погаснуть. Изобразим состояния цепи управления лампой таблицей состояния

х1	х2	у	х1	х2	у
		0 — не горит 1 — горит			0 — не горит 1 — горит

По таблице состояний теперь составим словесную модель цепи управления:

у — горит, если на х₁ есть воздействие И на х₂ нет воздействия;

у — горит, если на х₁ нет воздействия И на х₂ есть воздействие.

Изобразив нашу логическую фразу при помощи математических символов, мы будем иметь: у=х₁ х₂+ х₁ х₂ — это есть математическая модель управления объектом.

Схемная модель согласно правилам математической логики будет иметь вид, показанный на рис. 10.1, б. Анализируя схему, мы видим, что условие задачи на управление лампой от двух выключателей выполнено. Заметим,

что между х₁ верхним и х₂ нижним имеется жесткая механическая связь (показано пунктиром), т. е. если х₁ верхний замкнет цепь, то нижний разомкнет нижнюю цепь, и наоборот. Аналогично действует и х₂.

10.4. МАТЕМАТИЧЕСКИЕ СВОЙСТВА ЛОГИЧЕСКИХ ОПЕРАЦИЙ

Рассмотрим основные законы преобразования математических уравнений логических операций, которые в основном почти полностью сходны с обычными математическими преобразованиями.

1. Закон перемещения:

х₁х₂ = х₂х₁,

х₁+х₂ = х₂+х₁

2. Закон сочетания:

х₁(х₂x₃) = (х₁х₂)x₃

х₁+(х₂+x₃) = (х₁+х₂)+x₃·

3. Закон распределения:

х₁х₂ + х₁х₃ = х₁(х₂ + х₃) и, наоборот:

х₁(х₂ + х₃)= х₁х₂ + х₁х₃

4. Закон повторения:

х₁х₁х₁ = х₁

х₁ + х₁ + х₁ = х₁

5. Закон нулевого множества:

x ·0 = 0; х + 0 = х.

6. Закон универсального множества:

х ·1= х;

x+ 1=1

7. Закон дополнительности:

х₁х₁ = 0;

х₁+х₁ = 1;

8. Закон двойной инверсии:

х = х.

9. Закон инверсии:

Общая черта над произведением или суммой обозначает отрицание полученного результата.

Например, 1∙1 = 1, а наоборот 0, т. е. 1 · 1 =0.

Следует отметить, что закон инверсии и двойной инверсии широко применяется при синтезе схем управления.

Анализируя уравнения закона инверсии, можно сказать, что логическое умножение можно заменить логическим сложением, применяя контакты обратного действия, т. е. (х₁∙х₂) = х₁+х₂.

Доказательство этого закона можно изобразить таблицами состояния:

10. Закон поглощения:

х₁ (х₁ + х₂) = х₁

х₁ + х₁х₂ + х₁х₃ +...+ х₁х_n = х₁

11. Закон склеивания:

х₁х₂+х₁х₂ = х₁ х₁+х₁х₂ = х₁+х₂,

(х₁+х₂) (х₁+х₂) = х₁, х₁ + х₁х₂ =х₁+х₂

Есть и более сложные законы.

---

Дата добавления: 2015-08-27