Основные показатели качества АСР

Дифференциальное уравнение АСР, характеризующее изменение регулируемого параметра y(t) при изменении управляющего g(t) или возмущающего воздействия f(t), можно представить в виде

(a ₀ Рⁿ +... + а_п) у = (b₀Р^m +... + b_m) g +

+ (С ₀ Р^K +.... + C_k) f, (9.13)

где P = d/dt; С ₀, С ₁,.., C_k — коэффициенты полинома возмущающего воздействия.

Для следящих и программных АСР, да и АСР стабилизации наибольший интерес представляет качество переходных процессов, вызванных изменением управляющего воздействия g(t). Поэтому рассмотрим вопрос построения процесса регулирования, вызванного изменением g(t). Возвратимся к рис. 9.2. Показатели качества переходного процесса: Δ y _Д — динамический заброс или перерегулирование; t _п — время переходного процесса; Δ Y _уст — установившаяся (статическая ошибка) регулирования, а также колебательность переходного процесса весьма часто неблагоприятно влияют на качество выпускаемых изделий, показатели технологии.

Для определения показателей качества переходного процесса при данных настройках регулятора можно выполнить прямое решение дифференциального уравнения АСР (9.11) при f (t)=0, и при заданных математических законах изменения управляющего воздействия g(t). При этом получается y _B (t) — частное решение дифференциального уравнения с правой частью, характеризующее установившееся значение регулируемой величины Y _уст и величины ошибки Δ Y _уст. Получается также и y _п(t)—общее решение дифференциального уравнения без правой части, характеризующее переходный процесс в АСР и ве-

личины перерегулирования Δ y _д, время переходного процесса t _п и его колебательность. Подобные решения дифференциального уравнения, конечно, следует выполнять на ЭВМ. Несколько менее точно, но зато более быстро и наглядно можно выполнить анализ качества АСР на аналоговой вычислительной машине (АВМ). Вернемся к примеру АСР расхода воздуха при пневмотранспорте технологической щепы с использо-

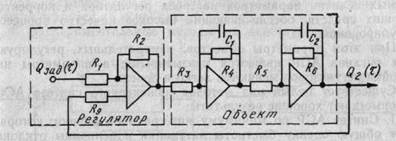
Рис. 9.6. Схема анализа на АВМ качества АСР расхода воздуха при пневмотранспорте технологической щепы

ванием пропорционального регулятора (см. рис. 9.3). Передаточная функция регулятора W(P) _рег = k_p объекта

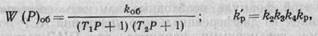
где k'_p —коэффициент усиления полного регулятора; k _об=1; Т ₁, Т₂ — постоянные времени. Все эти величины рассмотрены выше. На АВМ удобнее моделировать АСΡ по ее структурной схеме, выделяя на каждый элемент системы свой операционный усилитель аналоговой машины. Проводится соответствующее масштабирование реальных переменных на машинные переменные в виде электрических напряжений. На рис. 9.6 показана схема набора на ABM ACP расхода воздуха. Реальное время t заменяется на машинное τ. Величины сопротивлений и емкостей в цепях соответствующих операционных усилителей определяются известными соотношениями:

k'p = R ₂/ R ₁; T ₁= R ₄ C ₁; k _об=(R ₄/ R ₃)∙(R ₆/ R ₅); T ₂= R ₆ C ₂

Таким образом, подавая на вход схемы управляющее воздействие в виде электрического напряжения Q _зад(τ), на выходе получаем величину регулируемого параметра Q ₂(τ) в виде электрического напряжения в соответствующем масштабе. Q ₂(t) подается на осциллограф, который и показывает величины показателей качества АСР.

Дата добавления: 2015-08-27