Объекты автоматического регулирования технологических параметров

Процесс регулирования того или иного параметра должен характеризоваться устойчивостью, высоким быстродействием, невысокими отклонениями в переходных процессах, малыми и даже нулевыми ошибками в установившихся режимах. Задача решается правильным выбором типа и величин настроек регулятора.

Чтобы правильно выбрать тип регулятора и параметры его настройки (коэффициент усиления k_p, время изодрома t _и, время предворения t _пр ), необходимо иметь статические, динамические характеристики объекта регулирования, показатели ряда его свойств и условий работы. По передаточным функциям объекта, собственно, и находятся оптимальные настройки регулятора, обеспечивающие высокое качество регулирования. Динамические и статические характеристики объектов определяются аналитическим или экспериментальным путем. Наиболее распространенные промышленные объекты регулирования обладают в основном двумя обобщенными координатами, одна из которых представлят приток (расход) энергии или вещества, другая (выходная) однозначно определяет качество процесса. Кроме двух обобщенных координат, уравнение объекта включает и время t.

Поступательное движение механизма подачи лесопильной рамы, шпалорезного станка описывается уравнением

т(dv/dt)= F,

где т — масса; ν — линейная скорость; F — результирующая действующая сила.

Или вращательное движение пильного органа шпалорезного станка

I(d ω /dt)=M

где I — момент инерции; ω — угловая скорость; Μ — результирующий действующий момент.

При сушке пиломатериалов изменяется их влажность:

m_c(dw/dt)=W

где m _c — масса абсолютно сухой древесины в сушилке; w — относительная влажность древесины; W — масса влаги, удаляемой в единицу времени. Изотермическое заполнение (опорожнение) пневматического ресивера воздухом

(V/R γ )∙(dP/dt)=Q ρ= m

где V — объем ресивера; Ρ и ρ — давление и плотность воздуха; т и Q — массовый и объемный приход (расход) воздуха.

Иначе говоря, линейные модели объектов регулирования

описываются обобщенным уравнением L(dy/dt)= х. Величина у

характеризует регулируемую величину объекта (процесса); величина х характеризует мгновенное значение результирующего энергетического воздействия или потока вещества. Естественно, величина х связана со значениями возмущающего и управляющего воздействия на процесс.

Величина L определяет собственные свойства объекта и характеризует интенсивность изменения во времени выходной величины у при данном значении х,(dy/dt) = x/L.

Параметр L в физическом смысле характеризует инертность процесса (механическую, гидравлическую, тепловую и т. д.) и называется коэффициентом емкости объекта. Предыдущую формулу перепишем в виде dy =(1/L)xdt или

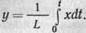
Подынтегральная функция характеризует элементарный поток энергии или вещества. При движении объекта — это

импульс силы Fdt или импульс момента Mdt, для пневматической емкости — импульс массы поступающего воздуха mdt.

Если проинтегрировать выражение

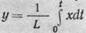
в пределах

времени, необходимого для изменения у на единицу, то получим, что коэффициент емкости L равен количеству вещества или энергии (подводимому за это время к объекту), необходимому для изменения выходной величины на единицу. Чем больше коэффициент емкости L, тем меньше чувствителен объект к приложенному воздействию, т. е. меньше меняется его параметр у при одном и том же воздействии х.

Каждому значению выходной координаты у отвечает определенный запас энергии или вещества, аккумулированного

в объекте U,

ПрИ L = Const, y ₁ =0 и y ₂= y,

U = Ly. Обобщенная величина U называется емкостью объекта. При поступательном движении U = mv, т. е. емкость равна количеству движения; при вращательном движении U = Ι ω, τ. е. моменту количества движения; для пневматического объекта U=VP/P γ, т. е. массе воздуха, содержащегося в ресивере.

Самовыравнивание — это свойство объектов регулирования, в силу которого при изменении нагрузки объекта (Q _п — притока или Q _p — расхода вещества или энергии) значение параметра у стремится без участия регулятора к новому установившемуся значению.

Большая степень самовыравнивания ρ способствует более быстрой стабилизации регулируемой величины и облегчает процесс регулирования.

Степень самовыравнивания определяется отношением увеличения или уменьшения подачи Q _п в процентах от ее величины при нормальном значении регулируемого параметра у _н к увеличению или уменьшению величины у в процентах от заданного значения.

В статических объектах, всегда обладающих самовыравниванием, каждому значению нагрузки соответствует определенное значение регулируемого параметра у. Астатические объекты регулирования не обладают самовыравниванием, при этом одному и тому же значению притока вещества или энергии Q _п могут соответствовать различные значения у, т. е. регулируемый параметр изменяется с постоянной скоростью, пропорциональной величине нарушения равновесия Δ Q притока и расхода вещества или энергии (Q _п— Q _p = Δ Q), например объекты регулирования уровня и др. Статические объекты описываются уравнениями усилительных, апериодических, колебательных звеньев. Астатические объекты — уравнениями интегрирующих звеньев.

Объекты регулирования иногда обладают транспортным (чистым) запаздыванием, характеризующимся временем τ, в течение которого величина у, несмотря на появившуюся разность (AQ = Q_n—Q_p), все же не изменяется; y = kx (t —τ), y = 0 при

t< τ.

Переходным (емкостным) запаздыванием процесса в объекте называется запаздывание, зависящее от тепловых, гидравлических, электрических сопротивлений между емкостями объекта. Емкостное запаздывание характеризуется постоянными времени Т.

Для одноемкостного объекта (апериодическое звено 1-го порядка) дифференциальное уравнение имеет вид (ТР+1) y = kx;

Р =d/dt;для двухъемкостного объекта (апериодическое звено

второго порядка) соответственно (Т₁Р+1) (Т₂Р+ 1) =kx имеются две постоянные времени Т₁, Т₂, и т. д. Коэффициент усиления объекта k есть отношение выходной величины у к входной x в установившемся режиме процесса.

Для многих объектов (электропривод, уровень в емкостях, объекты расхода вещества или энергии и др.) дифференциальные уравнения, статические и динамические характеристики определяются аналитически на основании известных закономерностей процессов.

Но для целого ряда объектов (гидротермообработка древесины, бассейны фанерных кряжей, пиловочного сырья, лесосу-шильные камеры и др.) для получения дифференциальных уравнений, динамических, статических характеристик приходится использовать экспериментальные методы.

Дата добавления: 2015-08-27