Устойчивость АСР

Это свойство АСР возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. В устойчивой АСР переходные процессы, вызванные изменением управляющего воздействия g (t), являются затухающими, при t→∞, y → y _ycт = const (рис. 9.4, α); в неустойчивой АСР — незатухающие (рис. 9.4, б),y→∞, причем переходные процессы изменения регулируемого параметра могут быть колебательными 1 или апериодическими 2. Следовательно, устойчивость— это работоспособность АСР.

Для анализа затухания или незатухания переходного процесса в АСР можно воспользоваться ее передаточной функцией

при f(t) = 0,

которая при нулевых условиях для P = d/dt имеет дифференциальное уравнение системы вида

[ 1 + W(P) _раз] y [ t ] = W(P) _раз g(t). (9.11)

Процесс регулирования определяется решением дифференциального уравнения (9.11) в виде суммы двух решений у (t) = = y _B (t)+у _П (t), y _B (t) — вынужденное (частное) решение дифференциального уравнения с правой частью, характеризует установившееся значение регулируемой величины y _ycт при t→∞; y_n(t) —общее решение дифференциального уравнения без правой части, характеризует интересующую нас переходную составляющую процесса регулирования. Известно, что переходная составляющая имеет решение

(9.12)

где С₁, С₂,..., С_п — постоянные интегрирования, определяемые из начальных условий; P ₁; Р ₂;...; Р_п — корни характеристиче-

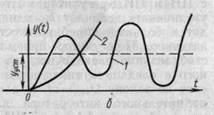
Рис. 9.4. Реакция устойчивых и неустойчивых АСР на скачкообразное изменение управляющего воздействия

ского уравнения 1 + W (P)_раз == a ₀ Pⁿ + а₁P^n-1 +... + а _n = 0; n — порядок дифференциального уравнения АСР.

Нетрудно видеть, что если корни будут вещественные и отрицательные (P₁ = —α ₁; Р₂ = —α₂;...; Р_п = —α _п), то при t-^oo составляющие уравнения (9.12) C₁e^{-α, t} →0,... C_ne^{-α nt} →0, т. е. y_n(t) → 0 и АСР будет устойчивой. Комплексные корни могут быть попарно сопряженными и при отрицательной вещественной части P_1,2 =—α± j β. При этом составляющие переходного процесса' (t → ∞) C ₁e^{-(α+ j β) t} +C ₂e^{-(α- j β) t} =A e^{-α t} sin(β t +φ)→0 затухают, что делает АСР устойчивой. При положительной вещественной части P_1,2=+α± j β, при (t → ∞) колебательные переходные составляющие будут расходящимися, АСР неустойчивой. Здесь А и φ — новые постоянные интегрирования. При наличии чисто мнимых корней Ρ₁=+ j β и Р₂ = — j β составляющая переходного процесса, определяемая этими корнями, будет представлять собой незатухающие колебания с постоянной амплитудой A, C ₁ ^{j β t} + C ₂e^{- j β t} = A sin (β t + φ) и АСР будет находиться на колебательной границе устойчивости.

Однако в практике анализа устойчивости АСР прямое решение исходного дифференциального уравнения (9.11) и определение корней характеристического уравнения не производится.

Существует несколько достаточно простых критериев устойчивости АСР. Но в основном используется частотный критерий Найквиста — Михайлова, который не только дает ответ об устойчивости или неустойчивости АСР, но и характеризует запасы устойчивости АСР по амплитуде (а) и фазе (γ).

Рассмотрим физический смысл этого критерия. При отсутствии возмущающих воздействий f (t)=0 в АСР искусственно разрывается обратная связь. Через задатчик в регулятор подается гармоническое синусоидальное управляющее воздействие g = A₁ sinω t (рис. 9.5, а). На выходе объекта в установившемся режиме появятся гармонические колебания регулируемого параметра у=А₂( ω ) sin (ω t +φ) той же частоты ω, но иной амплитуды Α₂( ω ) и сдвинутые по фазе на угол φ. Изменяют час-

тоту входного сигнала ω до величины ω_π, при которой сдвиг фазы выходного сигнала у будет φ = — π.

Если при частоте ω_π, (A ₂/ A ₁) > |—1|, то при одновременном замыкании обратной связи и снятии g (t)=0 в АСР возникнут расходящие колебания у, т. е. АСР будет неустойчивой (рис. 9.5, б). АФЧХ W (j ω)_раз охватывает точку с координатами — 1, j = 0. Если при частоте ω_π, Α₂/Α₁ = — 1, то при одновременном замыкании обратной связи и отключении g(t), g{t)= 0 в АСР возникнут незатухающие колебания одной амплитуды A ₂, АСР будет на колебательной границе устойчивости (рис.9.5,в).

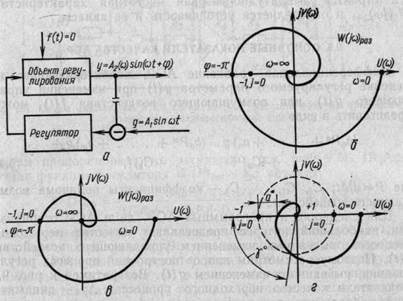
Рис. 9.5. Амплитудно-фазовые частотные характеристики АСР по критерию устойчивости Найквиста — Михайлова

Здесь АФЧХ W (j, ω)_раз проходит через точку с координатами комплексной плоскости —1, j = 0. И, наконец, если при частоте ω_π Α₂/Α₁< | — 1|, то при замыкании обратной связи и одновременном снятии сигнала g (t) в АСР, по понятным причинам, возникнут затухающие колебания, которые через некоторое время полностью исчезнут. Такая АСР будет устойчивой и ее АФЧХ в разомкнутом состоянии не будет охватывать точку с координатами —1, jV =0 (рис. 9.5, г). Этот рисунок наглядно характеризует запас устойчивости АСР по амплитуде а, запас по фазе γ°.

Сущность рис. 9.5, б, в, г, в общем-то, определяет математический аппарат построения АФЧХ W (j ω)_раз и определения запасов устойчивости.

Итак, имеется передаточная функция объекта, регулятора и АСР в разомкнутом состоянии W (Р)_раз.

W(Р) _раз = W(P) _об W(P) _рег, заменим Ρ = j ω, получим W(j ω ) = W(j ω ) _об W(j ω ) _рег. Это выражение представляется в виде W (j ω)_раз= U (ω)+ jV (ω). Задаваясь значениями частоты входного сигнала ω = 0; 0,01; 0,1; 1; 10; 100;..., ∞ вычисляют соответствующие величины вещественной U (ω) и мнимой jV (ω) части. По полученным точкам на комплексной плоскости строится амплитудно-фазовая частотная характеристика W (j ω)_раз и определяется устойчивость и ее запасы.

Дата добавления: 2015-08-27