Проверка на устойчивость исходной САУ по критерию Гурвица и Найквиста

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210104. 09. 000. ПЗ  

Из пункта 3 получили характеристический полином:

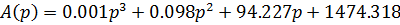
Для того, что бы составить определитель Гурвица надо по диагонали от левого верхнего до правого нижнего элемента матрицы выписать все коэффициенты. Пустые строки заполняем так, что бы чередовались строки с нечетными и четными индексами и когда коэффициент отсутствует на его месте пишем 0. Строим определитель Гурвица:

По определению САУ устойчива, если определитель Гурвица и все его диагональные миноры положительны:

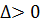
Отсюда следует, что САУ является устойчивой.

По Найквисту:

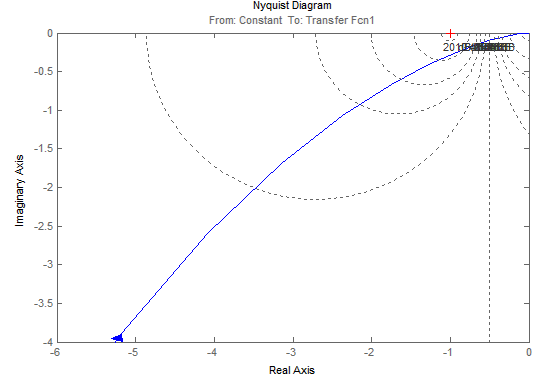
Рис.7. Увеличенный участок АФЧХ разомкнутой САУ

Годограф АФЧХ не охватывает точку с координатами (-1;j0) и движется по часовой стрелке, поэтому по критерию Найквиста САУ устойчива.

Запас по фазе на частоте единичного усиления: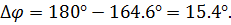

Запас по амплитуде: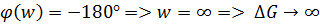

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210104. 09. 000. ПЗ  

6.Моделирование переходных характеристик исходной САУ

1.) При отсутствии возмущений для граничных значений g. Структурная схема для моделирования в MatLab представлена на рис.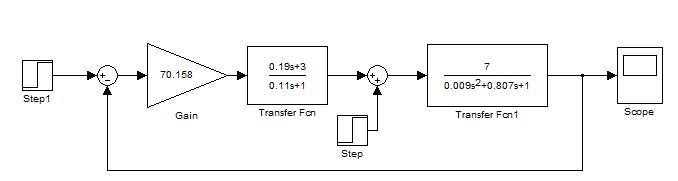

Рис.8. Схема исходной САУ в MatLab

1.1.) Здесь g не изменяется и равно своему минимальному значению 2.3, возмущающее воздействие z тоже равно своему минимальному значению 0. Результат моделирования представлен на рис.9.

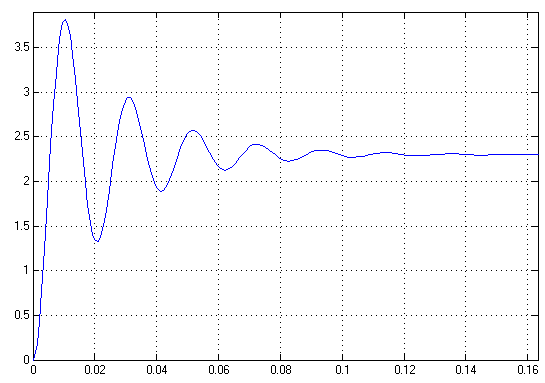
Рис.9. Результат моделирования при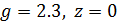

Время переходного процесса: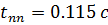

Перерегулирование:

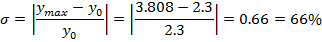
Колебательность: N=10

Время регулирования: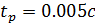

Период колебаний: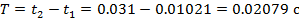

Логарифмический декремент затухания

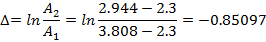
Частота колебаний:

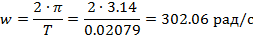
Коэффициент затухания:

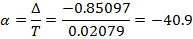
Декремент затухания:

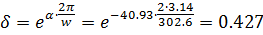
Как видим, частота () и декремент затухания (0,426 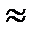0,427) имеют погрешность << 1% с ранее рассчитанными по п. 3, тем самым мы доказали правильность выполнения расчетов.

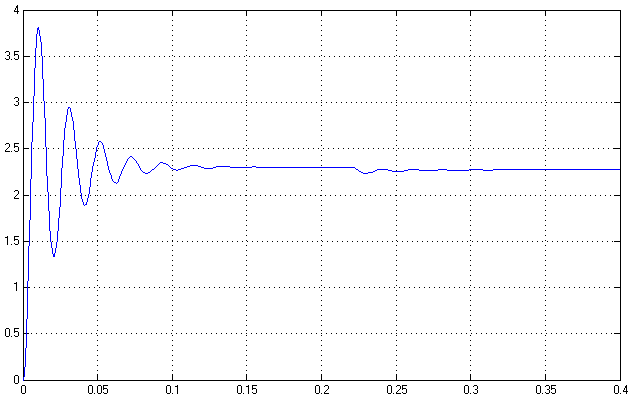
1.2.) Здесь g не изменяется и равно своему максимальному значению 13, возмущающее воздействие z равно своему минимальному значению 0.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210104. 09. 000. ПЗ  

Результаты моделирования представлены на рис.10.

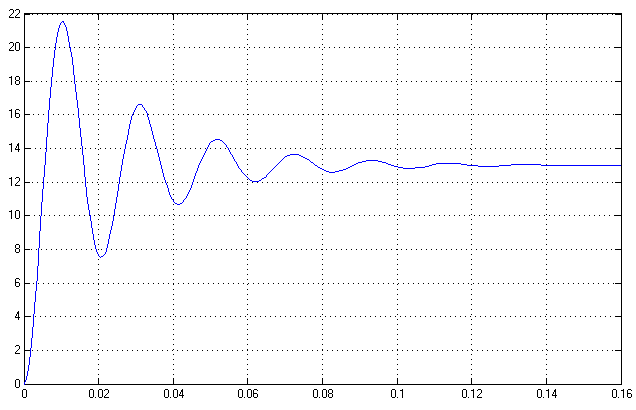
Рис.10. Результат моделирования при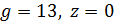

Время переходного процесса: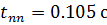

Колебательность: N=10

Время регулирования: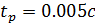

Перерегулирование:

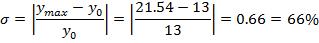
2.)При действующих максимальных и минимальных возмущениях z для граничных значений g.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210104. 09. 000. ПЗ  

2.1.) Здесь g равно минимальному значению 2.3, возмущающее воздействие z сначала равно своему минимальному значению 0, а в момент времени t=0.22 скачкообразно изменяется до z=-5. Результаты моделирования представлены на рис.11.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210104. 09. 000. ПЗ  

Рис.11. Результат моделирования при

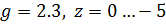
Время переходного процесса: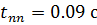

Время регулирования: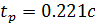

Колебательность: N=4

Максимальная динамическая ошибка:

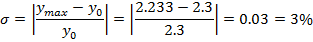
2.2.) Здесь g равно максимальному значению 13, возмущающее воздействие z сначала равно своему минимальному значению 0, а в момент времени t=0.22 скачкообразно изменяется до z=-5. Результаты моделирования представлены на рис.12.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БГТУ. 210104. 09. 000. ПЗ  

Рис.12. Результат моделирования при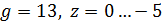

Так как величина возмущений не превышает коридор статизма, то можно считать, что переходный процесс по возмущению отсутствует.

Дата добавления: 2015-08-27