Читайте также:
|
Имея представление о статических характеристиках элементов и зная их взаимосвязь внутри САУ, можно получить представление о САУ в целом. Внешняя статическая характеристика САУ – это зависимость выходного сигнала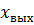 
от контролируемых возмущений z.
Запишем уравнение для данной САУ на основе ее структурной схемы:
При gmin=2.3
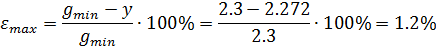
| z | -5 | |
| y | 2.2977 | 2.2720 |
При g=7.65
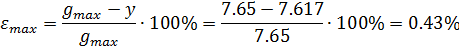
| Z | -5 | |
| y | 7.642 | 7.617 |
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| БГТУ. 210104. 09. 000. ПЗ |
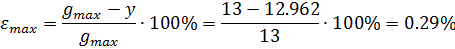
| z | -5 | |
| y | 12.987 | 12.962 |
Внешние статические характеристики САУ представлены на рис.2.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| БГТУ. 210104. 09. 000. ПЗ |
Рис.2 Внешние статические характеристики САУ
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| БГТУ. 210104. 09. 000. ПЗ |
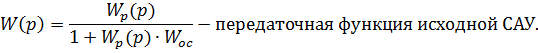
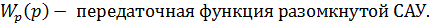
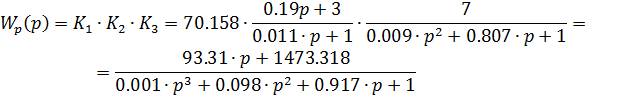
Так как обратная связь единична, то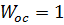 
, значит
Знаменатель передаточной функции - это характеристический полином системы: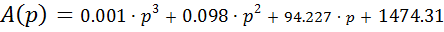 
Корни этого полинома определяют вид и параметры переходной характеристики САУ. Решая кубическое уравнение в среде MathCAD, получаем корни:
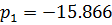
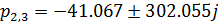
Так как вещественные части всех корней характеристического уравнения отрицательны, то можно сделать вывод о том, что система устойчива.
Кроме того, вещественные части комплексно-сопряженных корней отрицательны, что говорит о наличии затухающих колебаний с частотой 
, периодом 
, коэффициентом затухания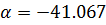 
и декрементом затухания
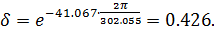
Дата добавления: 2015-08-27; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ | | | Расчет и построение частотных характеристик эквивалентной разомкнутой САУ: АФЧХ, ЛАЧХ, ЛФЧХ |