Опционные стратегии

Под стратегией в опционах понимается комбинация различных опционов и возможного базового актива в одном инвесторском портфеле. В зависимости от всевозможных сочетаний открываемых позиций различаются стратегии, указанные на рисунке 3 и множество других, не указанных на нём.

E z5wmK65qyFIQnK+zlHmv4T7JFMiykP8/KH8AAAD//wMAUEsBAi0AFAAGAAgAAAAhAJNevZL7AAAA 4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEA OP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAsAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA zhFC8nYTAABUDwEADgAAAAAAAAAAAAAAAAArAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAA ACEAt72MD90AAAAJAQAADwAAAAAAAAAAAAAAAADNFQAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAE AAQA8wAAANcWAAAAAA== ">

Рисунок 3 – Варианты опционных стратегий

1. Комбинационной называется каждая опционная стратегия, которая заключается в покупке call и put опционов, имеющих одинаковые базисные активы и дату истечения, при этом страйки могут быть как одинаковыми, так и нет (таблица 1). Например, если трейдер воспользовался комбинационной стратегией стрэнгл, это означает, что он одновременно завладел опционом на покупку (колл) акций «IBM» по цене $19000 и опционом на продажу (пут) тех же акций по цене $20000, оба опциона истекают в июне.

2. При использовании спрэд трейдер одновременно открывает две противоположные позиции на один и тот же вид опциона с одинаковым активом. Например, одновременная покупка и продажа put - опциона на акции «IBM» будет являться спрэдом.

3. Но наиболее распространены так называемые синтетические стратегии: сочетание купли (продажи) опционов с куплей (продажей) базисных активов.

Таблица 1 – Виды комбинационных стратегий

Название	Покупка	Продажа	Совпадение
call	put	call	put	страйков	экспирации
Стрэдл			-	-	+	+
-	-
Стрэнгл			-	-	–	+
-	-
Стрэп			-	-	+ или –	+
-	-
Стрип			-	-	+ или –	+
-	-
Вертикальный спрэд		-		-	–	+
-		-
Горизонтальный спрэд		-		-	+	–
-		-
Диагональный спрэд		-		-	–	–
-		-

В выборе подходящей стратегии должны помочь следующие факторы:

— общее направление цены базового актива;

— время истечения опциона;

— уровень волатильности.

И вот здесь настал черед привести как можно больше разнообразных теоретических сведений о волатильности.

2.1. Понятие волатильности и методы её оценки

Волатильность цены акции – это величина, измеряющая неопределённость его будущих изменений. При увеличении волатильности возрастает вероятность, что цена акции будет как очень высокой, так и очень низкой. Это не может не порадовать владельцев опционов, для которых наиболее привлекательными являются опционы на такие акции, рынок которых отличается резкими и значительными колебаниями цен (например, как акции компаний, производящих компьютерное оборудование и программное обеспечение). По мере увеличения этой привлекательности растёт и цена на опционы пут и колл. Различается 4 типа волатильности:

1. Истинная будущая волатильность – это то, что хотелось бы знать сегодня, но что станет известно только по прошествии данного периода.

2. Историческая (historical volatility).

3. Прогноз на определенный будущий период. Наиболее распространёнными методами прогнозирования являются так называемые EWMA и GARCH.

4. Ожидаемая или подразумеваемая волатильность (implied volatility).

Оценку исторической волатильности можно произвести на основе данных о цене актива за фиксированный промежуток времени. Его следует выбирать соразмерно с прогнозируемым периодом – это может быть неделя или месяц или год, в зависимости от числа дней, из которых состоит прогнозируемый период. Такой метод называется оценкой волатильности по ретроспективным данным. Пусть

годовая волатильность котировки актива;

r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> количество наблюдений;

цена акции в конце - го интервала, при ;

длина интервала в годах;

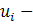доходность актива в - й интервал.

При этом

Обычная оценка стандартного отклонения для величин рассчитывается так:

Одновременно с этим стандартная оценка величин равна 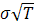. Отсюда следует, что является оценкой величины 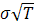. Поэтому, чтобы получить оценку 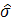величины волатильности 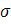, можно воспользоваться соотношением:

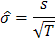
Стандартная ошибка будет приближенно равна .

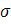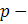На практике обычно используется подразумеваемая волатильность. Такой волатильность является величина , которая, если подставить её в формулу Блэка - Шоулза для вычисления первоначальных цен европейских опционов на бездивидендные акции, преобразует её в верное равенство. Вид этой формулы показан ниже ( цена опциона колл, опциона пут).

в которых

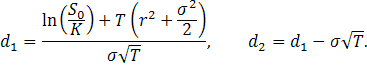
Функция 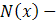это интегральная функция стандартизированного нормального распределения. Она представляет собой вероятность того, что случайная величина меньше величины в скобках . Для её вычисления можно применить полиномиальную аппроксимацию, но лучше этого не делать, а воспользоваться встроенной функцией НОРМСТРАСП в Excel.

количество операционных дней, оставшихся до истечения срока действия опциона, выраженное в годах (в году 252 операционных дня).

безрисковая процентная ставка (обычно соответствует ставке по государственным облигациям).

Для того, чтобы отыскать величину 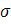, необходима итерационная процедура, в которой точность волатильности можно задать произвольно. Подразумеваемая волатильность используется для отслеживания мнений рынка об изменчивости цены конкретного актива.

Задача 2.1. Оценка волатильности по ретроспективным данным

Рассмотрим фьючерсный контракт на курс доллар США – российский рубль (USD/RUB), который торгуется на биржевом рынке FORTS. В таблице 2 представлены цены фьючерсов за последние 42 операционных дня ():

Таблица 2 – Расчёт доходности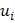

Дата	Цена последней сделки,	Дневная доходность
16.11.2011	31 385	-	-
17.11.2011	31 440	0,001751	3,07E-06
18.11.2011	31 441	3,18E-05	1,01E-09
21.11.2011	31 588	0,004665	2,18E-05
22.11.2011	31 642	0,001708	2,92E-06
23.11.2011	31 879	0,007462	5,57E-05
24.11.2011	32 039	0,005006	2,51E-05
…	…	…	…
03.01.2012	32 020	-0,01140	1,30E-04
04.01.2012	32 084	0,00200	3,99E-06
05.01.2012	32 342	0,00801	6,41E-05
06.01.2012	32 254	-0,00272	7,42E-06
09.01.2012	32 219	-0,00109	1,18E-06
10.01.2012	31 880	-0,01058	1,12E-04
11.01.2012	32 063	0,00572	3,28E-05
12.01.2012	31 851	-0,00663	4,40E-05
13.01.2012	32 110	0,008099	6,56E-05
Сумма	0,022837	1,93E-03

Теперь, когда необходимые суммы вычислены, определить оценку стандартного отклонения дневной доходности не составит труда:

Предположив, что число операционных дней в году – 252, а, значит, длина интервала оценка волатильности 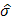соответствует значению

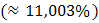со стандартной ошибкой .

Задача 2.2. Вычисление подразумеваемой волатильности

Стоимость колл - опциона на фьючерс на курс USD/RUB по итогам сессии 13.01.2012 составляла 750 руб. Текущий курс , страйк опциона рублей за 1000 долларов. Дата исполнения опциона 15.03.2012 (поэтому ). Безрисковая процентная ставка 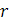по государственным облигациям не больше 8%.

Решение.

Чтобы найти приближённое значение подразумеваемой волатильности, воспользуемся самым простым из итерационных методов – половинного деления. Для этого в mathcad, задав все необходимые значения величин, напишем следующее:

– сnorm(х) — функция нормального распределения с параметрами

– взрастающая функция, поэтому необходимо выбрать значение .

– С = 750.

– значение волатильности с точностью .

Найденная подразумеваемая волатильность оказалась равной 9,096%. Должно быть, это значение выражает радужные надежды на то, что курс доллара будет более или менее постоянен какое - то время.

Дата добавления: 2015-08-26