Постановка задачи. Системы координат.

Рассматриваем следующую ситуацию на местности (рис. 2): c наблюдательным пунктом (НП),

находящимся в точке Н, связана прямоугольная декартовая система координат Нxy;

выбранное орудие находится в точке О с координатами (Пx,Пy). С орудием связана

прямоугольная декартова система координат Оuv; ось Оu-определяет основное направление

стрельбы орудия, ось Оv задает боковое (перпендикулярное) направление. Оси Оu и Оv являются т.н. главными осями рассеивания снарядов. Оси системы координат орудия развернуты относительно осей системы координат НП на некоторый угол Альфа.

Пусть орудие произвело n выстрелов по некоторой цели. центр которой находится в точке Ц

(на расстоянии Dist от точки О на оси Оu). Координаты точек падения снарядов (Xi,Yi), i= 1..n,

фиксируются не в системе координат орудия, а в системе координат НП, т.е., в системе Нxy.

Требуется по информации о n точках падения снарядов (Xi,Yi)в системе координат НП определить (дать оценки) следующих параметров стрельбы орудия:

- дальности до цели D относительно орудия;

-угла Альфа (угол разворота осей системы координат орудия относительно осей системы координат НП;

-точностных характеристик стрельбы орудия: срединных ошибок Вд и Вб.

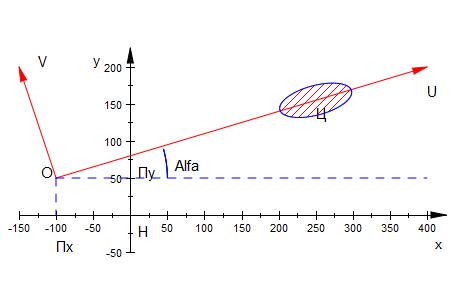
Рис.2

Дата добавления: 2015-08-20