Стрельба ударными снарядами. Основные формулы. Решаемые задачи.

Рассматриваем систему двух случайных величин (СВ) Xи Y (абсцисса и ордината точки падения снаряда),распределенных по нормальному закону. Главная формула- это формула плотности распределения вероятностей системы двух СВ- функция f(x,y). Эта функция получена из практики артиллерийских стрельб. Математически доказано и неоднократно проверено на полигонных испытаниях, что при стрельбе ударными снарядами СВ Xи Yявляются независимыми СВ. Для независимых СВ функция плотности распределения вероятностей имеет вид:

(1)

гдеxи y -координаты точки падения снаряда (абсцисса и ордината);

m_x,m_y -координаты центра рассеивания снарядов(ЦРС);

σ_x,σ_y -средние квадратические отклонения (СКО) по x и по yсоответственно;

Графиком функции f(x,y)является характерная симметричная холмообразная поверхность с центром в точке (m_x, m_y),рис.1

Рис.1

Основные свойства функции f(x,y):

1)f(x,y)≥0;

2)

(иначе не будет решаться главная задача-вычисление вероятности попадания в плоскостную цель)

3)СВ Xи Yнезависимы, если f(x,y)=f(x)∙f(y),т.е.

(2)

4). В сечении поверхности распределения плоскостями, параллельными плоскости xOy,получаются эллипсы.Покажем это.

Пересекаем поверхность z=f(x,y)плоскостью Z=Zo,параллельной плоскости xOy, где 0<Zo<Zmax;

где

,

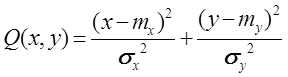
→ { берем логарифмы от обеих частей} →

→-(1/2)∙Q(x,y)=ln(2πσ_xσ_y);Q(x,y) =-2ln(2πσ_xσ_y);

{ Zo<Zmax, значит 2πσ_xσ_yZo<1=>т.е. ln(2πσ_xσ_y)<0}

И так как Q(x,y) оказывается при этом существенно положительной величиной, то ее можно обозначить h²:

Q(x,y)=h², где h²==-2ln(2πσ_xσ_y);

=> (3)

Уравнение (3) -это классическое уравнение эллипса с полуосями hσ_x и hσ_yи сцентром

В точке (m_x,m_y). При h=1 имеем т.н. единичный эллипс рассеивания, а при h=3 -полный эллипс рассеивания. Главная особенность: оси(полуоси) эллипсов рассеивания параллельны осям системы координат Oxy (т.е., осям системы координат орудия).Другими словами, при артиллерийской стрельбе ударными снарядами по плоскостной цели, эллипс рассеивания практически не поворачивается; оси симметрии эллипса параллельны координатным осям;

СВ X и Y независимы и некоррелированы.

5). Решение главной задачи стрельбы: определение вероятности попадания в плоскостную цель

известной площади (размеров),-базируется на использовании функции f(x,y).

, где Ф(x)-табличная функция Лапласа

(интеграл вероятности).

6). Правило " трех сигма ":(для СВ X)

P(m_x<X<m_x+σ_x)=Ф(1)-Ф(0)=0.3413-0.000=0.341;

P(m_x+σ_x<X<m_x+2σ_x)=Ф(2)-Ф(1)=0.4773-0.3413=0.136;

P(m_x+ 2σ_x<X<m_x+3σ_x)=Ф(3)-Ф(2)=0.498-0.4773=0.021;

Это означает, что для нормально распределенной СВ все рассеивание (с точностью до

долей процента) укладывается на участке m±3σ

1.2 Артиллерийская форма нормального закона:

Вместо средних квадратических отклонений σ_x и σ_y вводятся вероятные (срединные) отклонения Ex, Ey или Вд, Вб.

Вероятным(срединным) отклонением СВ X, распределенной по нормальному закону,называется половина длины участка, симметричного относительно центра рассеивания,вероятность попадания в который равна 0.5.Геометрическая интерпретация вероятного отклонения показана на рис.3.Вероятное отклонение Е-это половина длины участка оси абсцисс, симметричного относительно точки m, на который опирается половина площади кривой распределения.

Смысл термина " срединное отклонение,срединная ошибка ": Вероятность того, что СВ X отклонится от центра рассеивания m меньше, чем на Е, по определению вероятного отклонения Е,

равна 0.5: P(│X-m│ <E)=0.5.

Вероятность того, что СВ X отклонится от m больше чем на Е, тоже равна 0.5.

Таким образом, при большом числе испытаний в среднем половина значений СВ X отклонится от m больше, чем на Е, а половина -меньше. Отсюда и термины " срединная ошибка"," срединное отклонение".

Вероятное отклонение, как характеристика рассеивания, находится в прямой зависимости от среднего квадратического отклонения σ.Эту зависимость легко установить.

P(m-Е<X<m+Е)=Ф((m+E-m)/σ)- Ф((m-E-m)/σ)=Ф(E/σ)-Ф(-E/σ)=2Ф(E/σ) =0.5

из зависимости 2Ф(E/σ) =0.5, находим (из таблицы функции Лапласа) E/σ =0.674.

Е=0.674σ. В артиллерийской практике чаще пользуются следующей формой зависимости Е от σ:

E=ρ√2 σ

Если в качестве характеристики рассеивания принято вероятное отклонение Е, то плотность

.нормального распределения записывается в виде:

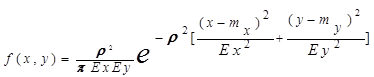(4)

если Вд,Вб, то

(5)

Формулы (4),(5) широко применяются в курсе ТОС.

Дата добавления: 2015-08-20