Нахождение точечных оценок

Проведем вычисление точечных оценок с помощью программы MATLAB:

Задаем значение n = 10

Нажимаем кнопку "провести расчеты" - получаем массив из 10 точек разрывов в пределах

полного эллипса рассеивания в системе координат НП и значения точечных оценок сразу для

всех требуемых параметров (Рис.3). На выходную форму также выведены и истинные значения

оцениваемых параметров (для оценки точности расчетов).

Рис.3

Точечные оценки для координат центра рассеивания снарядов в системе координат НП

находятся как средние арифметические значенияnчисел Xiи Yi:

;() ()

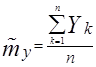Программа вычисления точечных оценок для координат центра рассеивания снарядов по

формулам ():

%Вычисление оценок мат.ожиданий

mx=0;my=0;

for k=1:n

mx=mx+X(k); my=my+Y(k);

end

mx=mx/n;

my=my/n;

%##########################################

= 5328.8 м 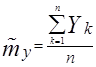= 4518.7 м

Истинные значения: m_x =5317.4 м, m_y =4513.4 м

Абсолютные ошибки: -m_x = 11.4 м; -m_y =5.3м.

Относительные ошибки: ( -m_x)/ m_{x* 100%} =0.25%

************************************************************

Найдем точечные оценки дисперсий и СКО случайных величин Xи Yпо формулам:

Ниже приведен фрагмент программы MATLAB,вычисляющий оценки дисперсий и СКО:

%##########################################

%Вычисление оценок дисперсий

DX=0;DY=0;

for k=1:n

DX=DX+(X(k)-mx)^2; DY=DY+(Y(k)-my)^2;

end

DX=DX/(n-1);DY=DY/(n-1);

Sigma_x=sqrt(DX);

Sigma_y=sqrt(DY);

%########################################

=1306.7 м² = 538.5 м²

Истинные значения: D_x =899.6 м², D_y =696.3м²

Абсолютные ошибки:a(x) =1306.7-899.6=407.1; a(y)=538.5-696.3=-157.8

Относительные ошибки:b(x)=a(x)/Dx*100%= 31%; b(y)=a(y)/Dy*100%= 22.6%

SigmaX =30м; SigmaY =26,4 м

*****************************************************************

Найдем точечную оценку корреляционного момента Kxyслучайных величин Xи Yпо формуле:

%Вычисление оценки корреляционного момента

Kxy=0;

for k=1:n

Kxy=Kxy+(X(k)-mx)*(Y(k)-my);

end

Kxy=Kxy/(n-1);

%################################

Оценка корреляционного момента Kxy =735.17;

Истинное значение корреляционного момента Kxyist =568.83

Абсолютная ошибка a(Kxy)=Kxyist -Kxy =735.17-568.83=166.34

Относительная ошибка b(Kxy)=a(Kxy)/Kxyist *100% =29%

********************************************************************

Найдем точечную оценку коэффициента корреляции rслучайных величин X и Y по формуле:

r =Kxy/SigmaX*SigmaY

%Вычисление оценки коэффициента корреляции r

r=Kxy/(Sigma_x*Sigma_y);

%#######################################

Оценка коэффициента корреляции r =0,87637;

Истинное значение коэффициента корреляции rist =0,7187

Абсолютная ошибка a(r)=0.87637-0.7187=0,1567

Относительная ошибка b(r)=a(r)/rist *100% = 22%

************************************************************************

Найдем точечную оценку угла ALFA

%################################

%Вычисление оценки угла ALFA

ALFA=atan2(2*Kxy,(DX-DY))/2;

%#######################################

Точечная оценка угла ALFA = 0.5446

Истинное значение ALFAist =0.697

Абсолютная ошибка a(ALFA) =ALFAist - ALFA =0,1524

Относительная ошибка b(ALFA) =0.3206/0.5236*100% =21,8%

*************************************************************************

Найдем точечные оценки для главных дисперсий средних квадратических отклонений, а

также для главных срединных ошибок:

%#######################################

%Вычисление оценок главных СКО

Sigma_x_GL=sqrt(DX*(cos(ALFA))^2+Kxy*sin(2*ALFA)+DY*(sin(ALFA))^2);

Sigma_y_GL=sqrt(DX*(sin(ALFA))^2-Kxy*sin(2*ALFA)+DY*(cos(ALFA))^2);

%##################################################################

Оценки для срединных ошибок Вд и Вб определяются по следующим зависимостям:

Вд=Sigma_x_GL * 0.674; Вб=Sigma_y_GL * 0.674

Точечные оценки: Вд =36,5 м; Вб =23,2м.

Истинные значения: Вд ist =25 м; Вб ist =15 м.

Абсолютные ошибки: а(Вд) =25 -36,5 =11,5 м; а(Вб) =10-23,2 =-13,2 м

Относительные ошибки: b(Вд) =11,5/25*100%=46%

b(Вб) =13,2/10*100% =132%

Задаем значение n = 20

Повторяем все вычисления -снова находим точечные оценки всех параметров стрельбы.

Нажимаем кнопку "провести расчеты" - получаем массив из 20 точек разрывов в пределах

полного эллипса рассеивания в системе координат НП и значения точечных оценок сразу для

всех требуемых параметров (Рис.4). На выходную форму также выведены и истинные значения

оцениваемых параметров (для оценки точности расчетов).

Рис.4

*********************************************************************************

Точечные оценки координат центра рассеивания снарядов в системе координат НП:

-= 5311,7м; =4513,5 м

Истинные значения: m_x =5317,4 м, m_y =4513,4 м

Абсолютные ошибки: а(mx)=5317,4-5311,7=5,7м; а(my)=4513,4-4513,5=0,1м.

Относительные ошибки: в(mx)=5,7/5317,4*100% =0.1%; в(my)=0,1/4513,4*100% =0.002%.

************************************************************

Точечные оценки СКОслучайных величин Xи Y:

SigmaX =33,65м; SigmaY =25,15м.

Истинные значения: SigmaXist =29,99м; SigmaYist =26,4м.

Абсолютные ошибки:a(x) =29,99-33,65=3,66м; a(y)=26,4-25,15=1,25

Относительныеошибки:b(x)=a(x)/SigmaXist*100%=12 %; b(y)=a(y)/SigmaYist*100%=5%.

****************************************************************************

Оценка корреляционного момента Kxy =670,547;

Истинное значение корреляционного момента Kxyist =568,835

Абсолютная ошибка a(Kxy)=Kxyist -Kxy =568,535-670,547=101,7

Относительная ошибка b(Kxy)=a(Kxy)/Kxyist *100% =17,9%

*************************************************************************

Оценка коэффициента корреляции r =0.79215;

Истинное значение коэффициента корреляции rist =0.7187

Абсолютная ошибка a(r)=0.7187-0,79215=0,073

Относительная ошибка b(r)=a(r)/rist *100% = 10%

********************************************************************

Точечная оценка угла ALFA = 0.6069

Истинное значение ALFAist =0.697

Абсолютная ошибка a(ALFA) =ALFAist - ALFA =0,09

Относительная ошибка b(ALFA) =0.09/0,697*100% =12,9%

Оценки для срединных ошибок Вд и Вб:

Точечные оценки: Вд =26,9м; Вб =8,7м.

Истинные значения: Вд ist =25 м; Вб ist =10м.

Абсолютные ошибки: а(Вд) =25 -26,9=1,9м; а(Вб) =10 -8,7 =1,3 м

Относительные ошибки: b(Вд) =1,9/25*100% =7,6%

b(Вб) =1,3/10*100% =13%

Задаем значение n = 200

Повторяем все вычисления -снова находим точечные оценки всех параметров стрельбы.

Нажимаем кнопку "провести расчеты" - получаем массив из 200 точек разрывов в пределах

полного эллипса рассеивания в системе координат НП и значения точечных оценок сразу для

всех требуемых параметров (Рис.5). На выходную форму также выведены и истинные значения

оцениваемых параметров (для оценки точности расчетов).

Рис.5

*********************************************************************************

Точечные оценки координат центра рассеивания снарядов в системе координат НП:

-= 5318,2м; =4514м

Истинные значения: m_x =5317,4 м, m_y =4513,4 м

Абсолютные ошибки: а(mx)=5317,4-5317,2=0,8; а(my)=4513,4-4514 =0,6м.

Относительные ошибки: в(mx)=0,8/5317,4*100% =0.015%; в(my)=0,6/4513,4*100% =0.013%.

************************************************************

Точечные оценки СКОслучайных величин Xи Y:

SigmaX =29,3м; SigmaY =28м.

Истинные значения: SigmaXist =29,99м; SigmaYist =26,4м.

Абсолютные ошибки:a(x) =29,99-29,3=0,69м; a(y)=26,4-28=1,6м

Относительныеошибки:b(x)=a(x)/SigmaXist*100%= 2,3%; b(y)=a(y)/SigmaYist*100%= 6%.

****************************************************************************

Оценка корреляционного момента Kxy =608,68;

Истинное значение корреляционного момента Kxyist =568,83

Абсолютная ошибка a(Kxy)=Kxyist -Kxy =568,83-608,68=39,85

Относительная ошибка b(Kxy)=a(Kxy)/Kxyist *100% =7%

*************************************************************************

Оценка коэффициента корреляции r =0,74009;

Истинное значение коэффициента корреляции rist =0.7187

Абсолютная ошибка a(r)=0.7187-74009=0,02

Относительная ошибка b(r)=a(r)/rist *100% = 0,002%

********************************************************************

Точечная оценка угла ALFA = 0.7547

Истинное значение ALFAist =0.697

Абсолютная ошибка a(ALFA) =ALFAist - ALFA =0,05

Относительная ошибка b(ALFA) =0.05/0,697*100% =8,3%

Оценки для срединных ошибок Вд и Вб:

Точечные оценки: Вд =25,5м; Вб =9,8м.

Истинные значения: Вд ist =25 м; Вб ist =10 м.

Абсолютные ошибки: а(Вд) =25 -25,5 =-0,5; а(Вб) =10 -9,8 =0,2м

Относительные ошибки: b(Вд) =0,5/25*100% =2%

b(Вб) =0,2/10*100% =0,2%

Задаем значение n = 2000

Повторяем все вычисления -снова находим точечные оценки всех параметров стрельбы.

Нажимаем кнопку "провести расчеты" - получаем массив из 2000 точек разрывов в пределах

полного эллипса рассеивания в системе координат НП и значения точечных оценок сразу для

всех требуемых параметров (Рис.6). На выходную форму также выведены и истинные значения

оцениваемых параметров (для оценки точности расчетов).

Рис.6

*********************************************************************************

Точечные оценки координат центра рассеивания снарядов в системе координат НП:

-= 5316,3 м; =4512,5м

Истинные значения: m_x =5317,4 м, m_y =4513,4м

Абсолютные ошибки: а(mx)=5317,4-5316,3 =1,1м; а(my)=4513,4-4512,5 =0,9м.

Относительные ошибки: в(mx)= 1,1/5317,4*100% =0.02%.в(my)=0,9/4513,4*100%=0,02%.

************************************************************

Точечные оценки СКО случайных величин Xи Y:

SigmaX =30,2м; SigmaY =27,1м.

Истинные значения: SigmaXist =29,99м; SigmaYist =26,4м.

Абсолютные ошибки:a(x) =29,99-30,2=0,2м; a(y)=26,4-27,1=0,7м

Относительныеошибки:b(x)=a(x)/SigmaXist*100%= 0,7%; b(y)=a(y)/SigmaYist*100%= 2,6%.

****************************************************************************

Оценка корреляционного момента Kxy =613,472;

Истинное значение корреляционного момента Kxyist =568,835

Абсолютная ошибка a(Kxy)=Kxyist -Kxy =568,835-613,742=45

Относительная ошибка b(Kxy)=a(Kxy)/Kxyist *100% =7,9%

*************************************************************************

Оценка коэффициента корреляции r =0.7492;

Истинное значение коэффициента корреляции rist =0.7187

Абсолютная ошибка a(r)=0.7197-0,7492=0,03

Относительная ошибка b(r)=a(r)/rist *100% = 4,2%

********************************************************************

Точечная оценка угла ALFA = 0.71246

Истинное значение ALFAist =0.697

Абсолютная ошибка a(ALFA) =ALFAist - ALFA =0,015

Относительная ошибка b(ALFA) =0.015/0.697*100% =2,15%

Оценки для срединных ошибок Вд и Вб:

Точечные оценки: Вд =25.6м; Вб =9.6м.

Истинные значения: Вд ist =25 м; Вб ist =10 м.

Абсолютные ошибки: а(Вд) =25 -25,6=-0.6м; а(Вб) =10 -9.6 =0.4м

Относительные ошибки: b(Вд) =0.6/25*100% =2,4%

b(Вб) =0.4/10*100% =4%

Дата добавления: 2015-08-20