
|
Читайте также: |
Пусть n–число сторон многоугольника.
1) Сумма внутренних углов многоугольника:
(n – 2) 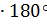 ;
;
2) Сумма диагоналей:
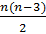 ;
;
3) Площадь правильного мнгоугольника:
S = 
где а – сторона правильного многоугольника.
Произвольный выпуклый четырехугольный

 ;
;
 ;
;
Параллелограм
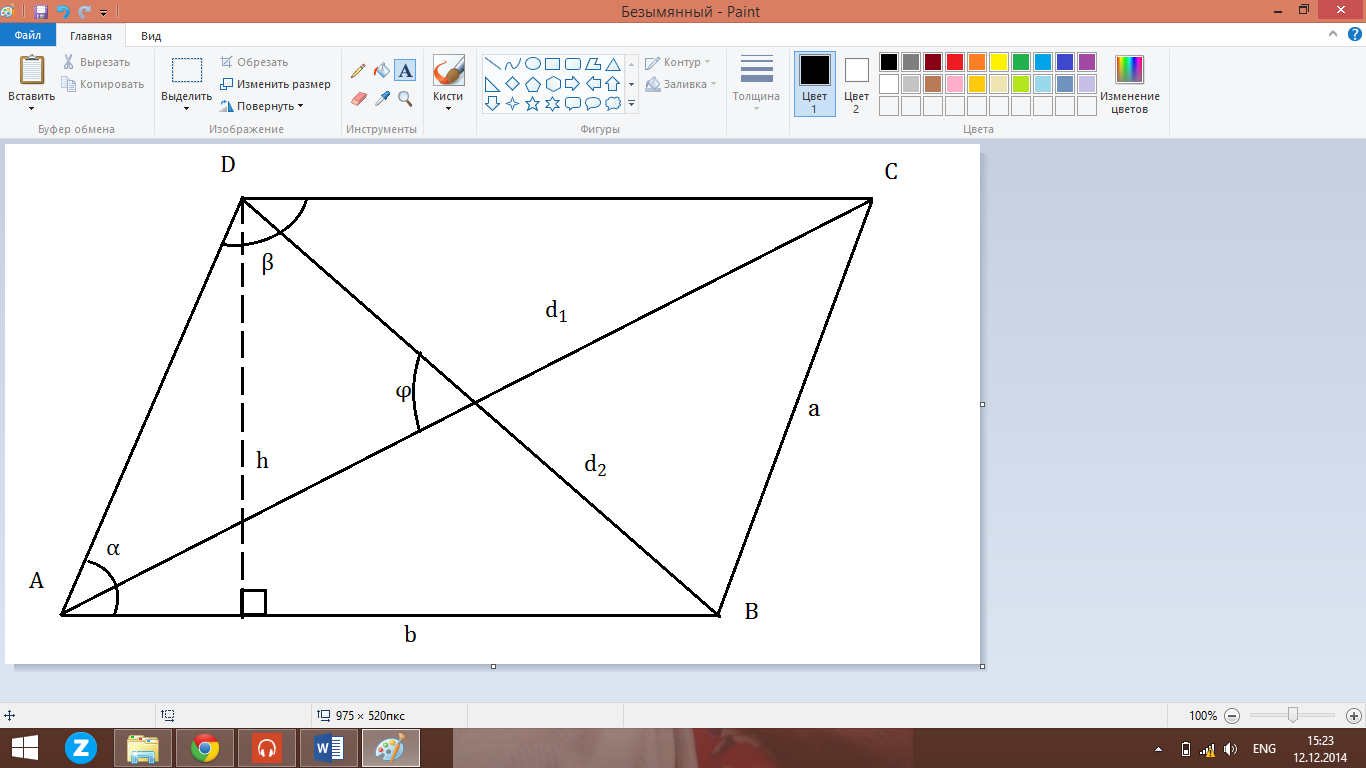
 ;
;
 ;
;
 ;
;
Дата добавления: 2015-08-17; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные свойства призвольного труегольника | | | Окружность. Круг. Сектор. Кольцо |