Модель исправления ошибок

6. ECM – error correction model.

В динамических регрессионных моделям важно различать долгосрочную и краткосрочную динамику.

- модель ADL(1,1) (8)

• В долгосрочном аспекте:

Пусть установились стационарные уровни Х и У ():

перестала фигурировать, т.к. устанавливается стационарный уровень.

(14)

(15)

Эта модель описывает долгосрочное стационарное состояние экономического процесса. - это коэффициент долгосрочного влияния X на Y.

• Модель ADL(1,1) можно привести к виду, который отражает краткосрочную динамику экономической системы, и таким образом получаем так называемую модель исправления ошибок.

Для этого из выражения (8) нужно вычесть в левой и в правой части. Затем вычесть и прибывать , тогда получим:

= с учетом (15) =

это модель исправления ошибок.

Трактовка модели: Если в предыдущий период переменная Y отклонилась от своего долгосрочного значения , то член () корректирует динамику в нужном направлении. Но для этого необходимо, чтобы . Бывает, что из теории известно, что . И часто именно такую модель называют ECM.

Несложно увидеть, что модель частично приспособления и модель адаптивных ожиданий является частным случаем исправления ошибок, причем не только формально математически, но и по экономическому смыслу.

Например, модель частичного приспособления в форме ECM выглядит следующим образом:

:

29.МоделиСАМР

Модель оценки финансовых активов предполагает, что: трансакционные издержки отсутствуют; все активы обращаются на открытом рынке; а инве­стиции бесконечно делимы (т. е. можно купить любую долю от единицы данного актива). Кроме того, предполагается возможность свободного дос­тупа к одной и той же информации для всех инвесторов, и из этого следует, что инвесторы не могут выявить на рынке переоцененные и недооцененные активы. Все эти предположения позволяют инвестору быть «диверсифици­рованным» без дополнительных издержек. В предельном случае их портфе­ли не только включат каждый из обращающихся на рынке активов, но и, помимо всего прочего, рискованные активы будут обладать одинаковыми весами (на основе их рыночной стоимости).

Тот факт, что в данный портфель включаются все обращающиеся на рын­ке активы, служит основанием для того, чтобы его называли рыночным пор­тфелем. В этом нет ничего удивительного, учитывая выигрыши от диверси­фикации и отсутствие трансакционных издержек в модели оценки финансовых активов. Если диверсификация сокращает степень подверженности риску на уровне фирмы, и отсутствуют издержки, связанные с добавлением дополни­тельных активов в портфель, то логическим ограничением диверсификации станет владение небольшой долей каждого из обращающихся активов в эко­номике. Если это определение кажется слишком абстрактным, представим себе, что рыночный портфель представляет собой очень хорошо диверсифициро­ванный взаимный фонд, который держит акции и реальные активы. В моде­ли САРМ все инвесторы будут держать комбинации, состоящие из более рис­кованного актива и этого взаимного фонда.

Портфели инвесторов в САРМ. Если все инвесторы на рынке имеют одина­ковые рыночные портфели, то каким образом выражается реакция инвесто­ров, обусловленная неприятием риска в совершаемых ими инвестициях? В модели оценки финансовых активов когда инвесторы при распределении средств решают: сколько им следует вложить в безрисковый актив, а сколь­ко — в рыночный портфель, они опираются на свои предпочтения в обла­сти риска. Инвесторы, избегающие риска, могут принять решение вложить все свои сбережения в безрисковый актив. Инвесторы, желающие принять на себя больше риска, вложат значительную часть своих сбережений, или даже все, в рыночный портфель. Инвесторы, уже вложившие все свои сред­ства в рыночный портфель и, тем не менее, желающие принять на себя еще больше риска, могли бы добиться этого, заняв средства по безрисковой ставке и инвестировав их в тот же самый рыночный портфель, следуя примеру всех остальных.

Данные предположения основываются на двух дополнительных допуще­ниях. Во-первых, существует безрисковый актив, ожидаемый доход которо­го известен с абсолютной определенностью. Во-вторых, инвесторы могут ссужать и занимать средства по безрисковой ставке для достижения опти­мальности размещения средств. В то время как ссуда по безрисковой ставке не доставляет особых проблем (индивиду для этого достаточно приобрести казначейские векселя или казначейские облигации), получение ссуд по без­рисковой ставке может оказаться куда более затруднительным для отдель­ного лица. Существуют версии модели САРМ, позволяющие несколько смяг­чить эти допущения и, тем не менее, получить выводы, совместимые с моделью.

Измерение рыночного риска отдельного актива. Риск любого актива для инвестора — это риск, добавляемый данным активом к портфелю инвес­тора в целом. В мире САРМ, где все инвесторы владеют рыночным порт­фелем, риск отдельного актива для инвестора — это риск, который дан­ный актив добавляет к рыночному портфелю. На интуитивном уровне понятно, что если движение актива происходит независимо от рыночного портфеля, то этот актив не добавит слишком уж много риска к рыночно­му портфелю. Другими словами, большая часть риска данного актива яв­ляется специфическим риском фирмы, а потому может быть диверсифи­цирована. С другой стороны, если стоимость актива имеет тенденцию к росту одновременно с повышением стоимости портфеля, равно как и тен­денцию к падению при снижении стоимости рыночного портфеля, то ак­тив увеличивает риск портфеля. Такой актив обладает в большей степени рыночным риском и в меньшей — специфическим риском фирмы. Стати­стически, добавленный риск измеряется ковариацией актива с рыночным портфелем.

Поскольку ковариация рыночного портфеля с самим собой является его дисперсией, бета рыночного портфеля (также как и его среднего актива) равна 1. Активы, чья рискованность выше среднего уровня (если использо­вать эту меру риска), будут иметь коэффициент бета выше единицы, а ак­тивы, которые безопаснее среднего уровня, будут обладать бетой менее еди­ницы. У безрисковых активов коэффициент бета равен нулю.

Получение ожидаемых доходов. Факт удержания каждым инвестором не­которой комбинации безрискового актива и рыночного портфеля приводит к заключению, что ожидаемый доход на актив линейно зависит от беты актива. В частности, ожидаемый доход на актив можно записать как функ­цию безрисковой ставки и беты этого актива:

Для использования модели оценки финансовых активов нам необходи­мо иметь три входные величины. Следующая глава будет посвящена деталь­ному разбору процесса оценки, поэтому пока только заметим, что каждая из этих входных величин оценивается следующим образом.

■ Безрисковый актив определяется как актив, относительно которого инвестору с абсолютной определенностью известна ожидаемая доход­ность для временного горизонта анализа.

■ Премия за риск является премией, запрашиваемой инвесторами за ин­вестирование в рыночный портфель, включающий все рисковые ак­тивы на рынке, вместо инвестирования в безрисковый актив.

■ Коэффициент бета, который определяется как ковариация актива, по­деленная на дисперсию рыночного портфеля, измеряет риск, добавля­емый инвестицией к рыночному портфелю.

Таким образом, в модели оценки финансовых активов весь рыночный риск охватывается одним коэффициентом бета, измеренным по отношению к рыночному портфелю, который, хотя бы теоретически, должен содержать все обращающиеся на рынке активы пропорционально их рыночной стоимости.

30.ПрименениеРегрессионногоанализавпроцессаххеджирования.

Регрессио́нный (линейный) анализ — статистический метод исследования влияния одной или нескольких независимых переменных на зависимую переменную . Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.

Хеджирование (от англ. hedge — страховка, гарантия) — открытие сделок на одном рынке для компенсации воздействия ценовых рисков равной, но противоположной позиции на другом рынке. Обычно хеджирование осуществляется с целью страхования рисков изменения цен путем заключения сделок на срочных рынках.

Для того чтобы успешно осуществлять хеджирование, необходимо четко знать как зависят друг от друга имеющаяся открытая позиция банка и потенциальный инструмент, которым данная позиция будет хеджироваться. Одним из самых простых показателей степени зависимости двух показателей между собой является ковариация. Формула для вычисления ковариации выглядит следующим образом [11, стр. 222]:

, (2.1)

где x_i и y_i -, показатели, а и - средние значения показателей.

Ковариационный анализ посвящен определению степени взаимо­связи двух рядов величин, которыми, в зависимости от рассматрива­емых инструментов, могут быть процентные ставки, обменные курсы и т. п. Если два ряда данных возрастают и убывают одновременно, то их ковариация является положительной. Если, однако, ряды являют­ся независимыми, то имеет место нулевая ковариация. При противо­положном изменении обоих рядов ковариация является отрицатель­ной.

Ковариации нескольких переменных удобно отражать в виде дисперсионно-ковариационной матрицы.

Коэффициент корреляции удобнее использовать, чем ковариацию, так как в нем преодолевается зависимость от числа наблюдений, кроме того, он независим от единиц измерения исследуемых величин.

Для исследований в основном используется линейный коэффициент корреляции, обычно называемый Пирсоновским коэффициентом корреляции, хорошо применимый для линейных связей.

Линейный коэффициент корреляции между двумя рядами Х и Y определяет­ся по следующей формуле [11, стр. 224]:

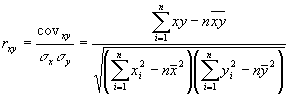
где σ_xи σ_y – среднеквадратичное (стандартное) отклонение значений рядов X и Y соответственно.

Коэффициенты корреляции также могут быть представлены в виде матриц. В таблице 2 показаны коэффициенты корреляции всех возможных пар из группы трех активов.

Рассмотрим регрессионный анализ для простой линейной зависимости между зависимой переменной Y и одной независимой X [15, стр. 262]:

Y = a + βХ+e, (2.6)

где α – постоянная, отражающая значение Y при X =0, β – коэффициент регрессии («бета»-коэффициент), e – ошибка или значение помехи (оценивает влияние других факторов, не включенных в модель).

Для статистической проверки взаимосвязи чаще других используется метод наименьших квадратов. Он дает наилучшие линейные несмещенные оценки.

Допущения при расчете:

- линейная зависимость между переменными;

- значение ошибки e_i нормально распределено со средней, равной нулю, и постоянной дисперсией σ²;

- значения e независимы друг от друга, т.е. факторы, которые послужили причиной ошибки для одной из величин Y, не приводят автоматически к ошибкам для всех наблюдений Y (т.е. данные неавтокоррелированы).

Коэффициенты можно найти по следующим формулам [15, стр. 270]:

, (2.7)

. (2.8)

Значение фактической ошибки e вычисляется как фактическая разница между фактическими значениями переменной y_i и рассчитанными значениями исходя из формулы линейной регрессии [11, стр. 233]:

Можно использовать как метод простой линейной, так и множест­венной регрессии. Множественную регрессию следует использовать для анализа зависимости между более чем двумя переменными. На­пример, зависимость между ценой облигации спот и ценой фьючер­сного контракта на облигацию и возможное внешнее влияние на эти инструменты, допустим, обменного курса. В этом случае линейная регрессионная зависимость между ценой облигации и ценой фьючерс­ного контракта имела бы следующую форму [7, стр. 13]:

Цена облигации Х =а+b* (Цена фьючерсного контракта)+

+с*(Курс конвертации Y)

При использовании регрессионных методов для определения коэффициентов хеджирования возникают следующие проблемы:

- «исто­рические» зависимости между двумя взаимосвязанными рядами про­центных ставок могут быть нестабильными, и имеющиеся критерии изменчивости цен могут быть не пригодными для прогнозирования относительной изменчивости цен в будущем;

- использование слишком короткого периода для исследования зависимости между инструмен­тами может быть недостаточным для получения результата, отражающего истинное положение дел (для инструментов с длительными сроками погаше­ния могут отсутствовать длинные ряды данных, если операции с эти­ми инструментами производились в течение лишь короткого периода времени)

31.МодельМонте-Карло

Дата добавления: 2015-08-17