Читайте также:
|
Определение 3. СЛАУ, вектор правых частей которой равен нулю: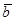 
= 0, называется однородной. В противном случае система называется неоднородной. Для однородных СЛАУ имеют место несколько общих утверждений.
Однородной системой линейных уравнений называется система вида: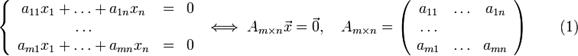 
Теорема 1. Однородная СЛАУ всегда совместна.{Нулевой вектор всегда является решением однородной СЛАУ} Теорема 2. Множество решений однородной СЛАУ образует линейное пространство. {Пусть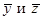 
− решения системы 
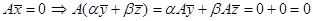, т.е. их линейная комбинация тоже решение. Выполнение аксиом − очевидно.}
Дата добавления: 2015-08-17; просмотров: 40 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Системы линейных алгебраических уравнений (СЛАУ). Различные формы записи СЛАУ. Совместные и несовместные СЛАУ. Доказательство критерия Кронекера—Капели совместности СЛАУ. | | | Санкт – Петербург |