Элементарные преобразования строк (столбцов) матрицы. Нахождение обратной матрицы методом элементарных преобразований.

При элементарных преобразованиях строк (столбцов) матрицы ее ранг не меняется. С помощью этих преобразований(умножение/деление на число, сложение строки с другой строкой, предварительно умноженной на любое число) можно так упростить матрицу, чтобы ранг новой матрицы легко вычислялся.

Рассмотрим метод нахождения обратной матрицы, основанный на элементарных операциях над строками.

Сначала составляется расширенная матрица – присоединением к матрице A единичной матрицы E:

Затем с помощью элементарных операций над строками расширенная матрица (A | E) преобразуется к виду (E | B). С формальной точки зрения такие преобразования могут быть реализованы умножением на матрицу A некоторой матрицы T, которая представляет собой произведение соответствующих элементарных матриц (матрицы перестановки, матрицы масштабирования, неунитарной матрицы): TA = E. Это уравнение означает, что матрица преобразования T представляет собой обратную матрицу для матрицы A: T = A-1. Тогда TE = A-1 и, следовательно,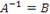

Теорема об инвариантности ранга матрицы относительно элементарных преобразований.Нахождение ранга матрицы методом элементарных преобразований.

Ранг матрицы инвариантен относительно элементарных преобразований (эквивалентные матрицы

имеют равные ранги). Для доказательства этого утверждения достаточно заметить, что

элементарные преобразования матрицы сохраняют ее ненулевые мино-

ры (они могут лишь изменить их знаки). {При указанных преобразованиях любой минор матрицы (как обычный определитель) может изменить свое значение только следующим образом: }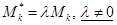

Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

Пример. Привести матрицу к ступенчатому виду.

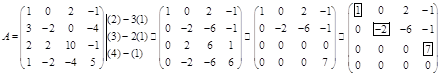
Дата добавления: 2015-08-17