Санкт – Петербург

Техникум геодезии и картографии

КОНТРОЛЬНАЯ РАБОТА № 2

По геодезии

Вариант № ______09_______

Выполнил:

студент___3__ курса___ПГ-11-13___группы

Смирнов Алексей Владимирович

Санкт – Петербург

Содержание

Часть первая

1. Прямая и обратная геодезическая задачи на плоскости, их назначение, практическое применение, вывод формул 3

2. Сформулировать главное условие, которое должно соблюдаться в нивелире. Вывести формулу определения величины «Х» и объяснить методику его исправления в нивелире НЗ 5

Часть вторая

3. Решить обратную геодезическую задачу 7

4. Вычислить координаты точек теодолитного хода, составить схему хода и вычертить её 8

5. Обработать страницу полевого журнала нивелирования IV класса и выполнить постраничный контроль 14

6. Обработать страницу полевого журнала нивелирования III класса и выполнить постраничный контроль 16

Прямая и обратная геодезическая задачи на плоскости, их назначение, практическое применение, вывод формул.

Прямая геодезическая задача. При решении таких задач требуется найти координаты конечной точки, зная координаты начальной точки, горизонтальное проложение и дирекционный угол направления.

При решении обратной геодезической задачи требуется найти дирекционный угол направления и величину горизонтального проложения, зная координаты двух точек.

Практическое применение прямой и обратной геодезических задач заключается в том, что с их помощью определяют точное местоположение объектов на карте (плане), относительно друг друга.

Рис.1

, где ХА,УА – координаты первой точки; ХВ,УВ – второй, α – дирекционный угол, D – горизонтальное проложение.

Для прямой геодезической задачи:

ХВ-ХА=∆Х, а УВ-УА=∆У, откуда ХВ=ХА+∆Х и УВ=УА+∆У. Следовательно формулы в общем виде:

Хn+1=Хn+∆Xn, а Уn+1=Уn+∆Уn.

Таким образом, координата последующей точки равняется координате предыдущей точке плюс приращение.

Из треугольника АВС(рис.1) следует, что ∆Х=D , а ∆У=D .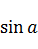

Знаки приращения координат определяются знаками и 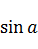(см.табл.1)

Таблица 1.

Четверть	Величина	Знак
∆Х	∆У
I	0˚- 90°	+	+
II	90˚- 180˚	-	+
III	180˚- 270˚	-	-
IV	270˚ - 360˚	+	-

Для решения обратной геодезической задачи требуется определить α – дирекционный угол. Tg α = , а следовательно α = arctg .

Горизонтальное проложение D, для контроля, вычисляют дважды. Из треугольника АВС(рис.1) следует, что D = 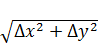. А так же D = = ∆У cosec α = ∆X sec α.

Сформулировать главное условие, которое должно соблюдаться в нивелире. Вывести формулу определения величины «Х» и объяснить методику его исправления в нивелире НЗ.

Рис.2

Главным условием нивелира является параллельность проекций оси цилиндрического уровня и визирной оси зрительной трубы на отвесную плоскость. Поверка данного условия осуществляется двойным нивелированием с концов линии длиной 75 метров, обозначенной костылями Аи В (рис 2,а,б). На одном конце линии устанавливают нивелир так, чтобы при визировании на рейку (костыль В) окуляр оказался на отвесной линии, проходящей через костыль А. Приводят ось вращения нивелира в отвесное положение с помощью круглого уровня. Визируют на рейку, вращая элевационный винт, приводят пузырёк уровня в нуль-пункт и берут отсчёт по рейке (a1). С помощью рейки (рулетки) измеряют по отвесной линии высоту нивелира i1, от вершины костыля до середины окуляра с точностью 1мм. Из рис.2,а следует, что

h=i1-(a1-x). (1)

После этого рейку и нивелир меняют местами и выполняют аналогичные наблюдения, в результате которых получают отчёты a2 и i2. Из рис.2,б видно, что

h=a2-x-i2. (2)

Из рис.2(а,б) видно, что величина h одна и та же, х – погрешность в отсчётах по рейке, вызванная непараллельностью визирной оси и оси цилиндрического уровня, будет одинакова, т.к. расстояние между костылями А и В осталось неизменным, так же не изменился угол между визирной осью и осью уровня. Следовательно:

i1-(a1-x)= a2-x-i2

2х=а1+а2-(i1+i2)

x= .

Если в результате вычислений оказалось, что х больше 4мм, то вращая элевационным винтом, наводят среднюю нить на отсчёт аʹ2=а2-х, соответствующий горизонтальной линии визирования (см.рис.2,б). Пузырёк цилиндрического уровня сместиться с нуль-пункта.

Ослабив боковые и регулируя вертикальными исправительными винтами уровня, привести пузырёк в нуль-пункт.

Поверку повторять до получения значения х≤4мм.

Решить обратную геодезическую задачу.

Даны координаты двух пунктов А и В. Вычислить дирекционный угол α направления АВ и длину стороны (дважды) между этими пунктами. Пункт А: Х(6166361,64),У(7297425,32); пункт В: Х(6166260,20),У(7297631,20).

Рассчитаем приращение координат:

∆Х=Хв-Ха

∆Х=6166260,20 - 6166361,64= -101,44

∆У=Ув-Уа

∆У=7297631,20 - 7297425,32=205,88

Тангенс дирекционного угла равен .

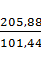= - . Т.к. ∆Х отрицательное, а ∆У положительное, то дирекционный угол находиться во второй четверти. Дирекционный угол α =116˚13'

Найдём длину стороны(D).

D=

D= 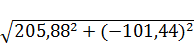=229,5139 метров.

Найдём длину 2-м способом.

D= = = 229,606

D= = =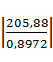229,469

Вычислить координаты точек теодолитного хода, составить схему хода и вычертить её.

Приращения координат вычислять и увязывать до 0,01м., координаты вычислять до 0,1м. После вычисления координат точек хода построить координатную сетку. Оцифровать её и нанести по координатам все точки хода.

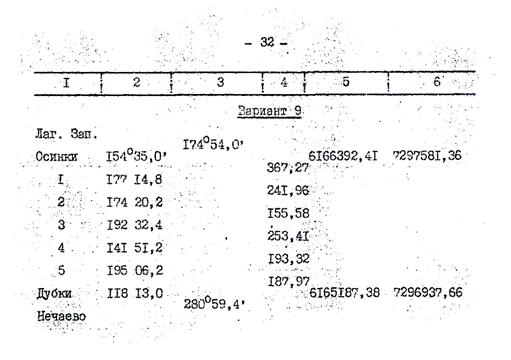
По условию задачи все углы теодолитного хода правые.

Используя формулу для подсчёта правых дирекционных углов поворота, которая в общем виде выглядит следующим образом:

αк=αн + 180˚ n.

Подсчитаем . В нашем случае она равна 1153˚52,8ʹ.

Подставим в общую формулу наши данные, при n=7 (количество углов).

174˚54,0ʹ- 1153˚52,8ʹ+180˚ = 174˚54,0ʹ+ 106˚07,2ʹ= 281˚01,2ʹ

Из-за неизбежных погрешностей угловых измерений αк вычисленное по формуле будет отличаться от заданного.

Угловая невязка хода (fß) определяется разницей между αк заданным и αк вычисленным.

280˚59,4ʹ- 281˚01,2ʹ= - 0˚01,8ʹ

Допустимое значение fß вычисляют по формуле:

fß = , в нашем случае fß =

Невязку необходимо устранить путём введения поправок. Исправление измеренных углов сводится к распределению между ними поровну угловой невязки, взятой с обратным знаком. Однако, не всегда найденная невязка делится на n без остатка. Тогда большие поправки вводятся в углы образованные более короткими сторонами.

В нашем случае углов 7, значит, вводим поправку +0˚00,2ʹ на каждый угол и дополнительно +0˚00,1ʹ на углы №1,№5,№6,№7, т.к. у них более короткие стороны относительно остальных углов.

Повторим вычисления с учётом поправки.

=154˚35,3ʹ +177˚15,0ʹ +174˚20,4ʹ +192˚32,6ʹ +141˚51,5ʹ + +195˚06,5ʹ+118˚13,3ʹ=1153˚54,6ʹ

αк=αн + 180˚ n

174˚54,0ʹ- 1153˚54,6ʹ+180˚ = 174˚54,0ʹ+ 106˚05,4ʹ= 280˚59,4ʹ

С учётом поправок: αк(исход)=αк(измер).

Вычислим дирекционные углы. Правые ищут по формуле: αпослед=αпредыд – ßисправ + 180˚

α1=174˚54,0ʹ- 154˚35,3ʹ+ 180˚=200˚18,7ʹ

α2=200˚18,7ʹ- 177˚15,0ʹ+ 180˚=203˚03,7ʹ

α3=203˚03,7ʹ- 174˚20,4ʹ+ 180˚=208˚43,3ʹ

α4=208˚43,3ʹ- 192˚32,6ʹ+ 180˚=196˚10,7ʹ

α5=196˚10,7ʹ- 141˚51,5ʹ+ 180˚=234˚19,2ʹ

α6=234˚19,2ʹ- 195˚06,5ʹ+ 180˚=219˚12,7ʹ

α7=219˚12,7ʹ- 118˚13,3ʹ+ 180˚=280˚59,4ʹ

αк(данное)=αк(вычисл), следовательно контроль показал, что вычисления верные.

Дальше по формулам прямой геодезической задачи вычисляют приращение координат.

Координаты точки рассчитывают следующим образом: хn=хn-1+∆х; уn=уn-1+∆у.

∆х=s ; ∆у=s , где s- горизонтальное проложение, - дирекционный угол.

Соответственно:

∆х1-2=367,27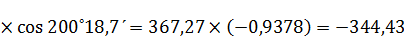

∆х2-3=241,96

∆х3-4=155,58

∆х4-5=253,41

∆х5-6=193,32

∆х6-7=187,97

∑∆хфакт.=

∑∆хданное=

∆у1-2=367,27

∆у2-3=241,96

∆у3-4=155,58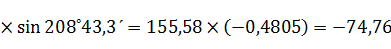

∆у4-5=253,41

∆у5-6=193,32

∆у6-7=187,97

∑∆уфакт=

∑∆уданное=

Рассчитаем невязку в приращении координат по оси у.

fу =∑∆уфакт - ∑∆уданное = 0,32

Теперь, по оси х.

fх =∑∆хфакт - ∑∆хданное= - 0,25

Вычислим абсолютную и относительную погрешности.

(абс)= 0,85

f(отн) =

Относительная линейная невязка считается допустимой, если её величина лежит в пределах от до . В нашем случае условие выполняется, следовательно уравниваем ∆х и ∆у вводя поправки с обратным знаком пропорционально длинам сторон хода. Поправка обозначается б.

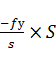б хi = i; б уi = i.

б х1 = ;

б х2 = 0,04; б х3 = 0,03; б х4 = 0,05; б х5 = 0,03; б х6 = 0,03.

б у1 = ;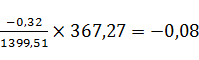

б у2 = 0,06; б у3 = 0,04; б у4 = 0,06; б у5 = 0,04; б у6 = 0,04.

Выполним контроль. Должны соблюдаться равенства: ∑∆хисправ = ∑∆хданное и ∑∆уисправ = ∑∆уданное.

∑∆хисправ = . Что равно ∑∆хданное.

∑∆уисправ = . Что равно ∑∆уданное.

По уравнениям приращения координат вычисляют координаты всех пунктов хода.

х1=хосинки+∆х1-2;у1=уосинки+∆у1-2

х1=6166392,41 6166048,05

у1=7297581,36 7297453,76

х2=х1+∆х2-3; у2=у1+∆у2-3

х2=6166048,05

у2=

х3=х2+∆х3-4; у3=у2+∆у3-4

х3=

у3=

х4=х3+∆х4-5; у4=у3+∆у4-5

х4=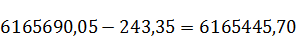

у4=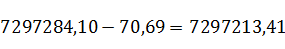

х5=х4+∆х5-6; у5=у4+∆у5-6

х5=

у5=

хдубки=х5+∆х6-7; удубки=у5+∆у6-7

хдубки=

удубки=

Координаты хдубки и удубки полученные в результате вычислений совпали с заданными, что и является контролем.

Схема теодолитного хода.

Обработать страницу полевого журнала нивелирования IV класса и выполнить постраничный контроль.

Дальномерные расстояния до задней и передней реек вычисляются вычитанием отчёта по дальномерному штриху из отчёта по чёрной стороне по средней нити соответствующей рейки.

Контролем качества наблюдений является сходимость дважды вычисленного превышения по чёрным (пч) и красным (пк) сторонам реек. Расхождение допускается не более 5мм с учётом разности высот нулей комплекта реек. Вычисляют среднее превышение (ср.п). Оно равно полусумме пч и пк с учётом разности высот реек.

На станции вычисляют разность высот пяток реек между отсчётом по чёрной стороне по средней нити и отсчётом по красной стороне для каждой рейки (рвз и рвп). Контролем вычислений на станции является равенство (рвз- рвп) = (пч – пк).

На каждой странице производят контрольные вычисления:

Сумму отсчётов по задней рейке по средней нити по чёрной и красной сторонам (∑зрчк) (54812);

Сумму отсчётов по передней рейке по средней нити по чёрной и красной сторонам (∑прчк) (37682);

Алгебраическую сумму превышений (асп) (17130);

Алгебраическую сумму средних превышений(ассп) (8565).

Итоговым контролем правильности вычислений является равенство асп = ∑зрчк - ∑прчк и ассп = 0,5асп.

17130 = 54812 – 37682

8565 = 0,5

Обработать страницу полевого журнала нивелирования III класса и выполнить постраничный контроль.

Обработку полевого журнала нивелирования III класса начинают с контроля наблюдения на станции.

1. Отсчёт по средней нити по чёрной стороне каждой рейки должен быть равен полусумме отсчётов по дальномерным штрихам. Допустимое расхождение 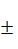3 мм.

2. Вычисляют разность отсчётов по чёрным сторонам задней и передней по крайним дальномерным нитям. В свою очередь, их разница это неравенство расстояний на станции от нивелира до реек (не более 20мм.).

Дважды вычисляют превышения на станции:

Отсчёт по чёрной стороне задней рейки минус отсчёт передней рейки; отсчёт по красной стороне задней рейки минус отсчёт передней рейки. При вычислении пользуются отсчётами средней нити. В свою очередь, разность превышений не должна быть более 3мм. с учётом разности высот нулей комплекта реек ( 100). Следом вычисляют среднее превышение. Оно равно полусумме превышения по чёрной и красной стороне ( 100).

Кроме того на станции вычисляют разность между отсчётами красной и чёрной сторон каждой рейки (по средней нити).Если из результата передней рейки вычесть результат задней, должна получиться величина равная разности превышений, что является одним из контролей правильности вычислений. Вторым контролем является тождество между неравенством расстояний на станции и результатом вычитания разностей отчётов по дальномерным штрихам задней и передней рейки соответственно.

По окончании полевой работы выполняют контрольные постраничные вычисления. В них входят:

Сумма отсчётов по дальномерным нитям по задней рейки(∑однзр)(15148);

Сумма отсчётов по дальномерным нитям по передней рейки(∑однпр)(20754);

Алгебраическая сумма контрольных превышений(аскп)(-5606);

Сумма отсчётов по средней нити по задней рейке(∑оснзр) (43528);

Сумма отсчётов по средней нити по передней рейке(∑оснпр) (49143);

Алгебраическая сумма превышений (асп)(-5615);

Алгебраическая сумма средних превышений(ассп) (-2806).

Величина ассп должна равняться 0,5 асп 3мм.

0,5

∑оснзр - ∑оснпр = асп

43528 – 49143 = - 5615

∑однзр - ∑однпр д.б. равно аскп

15148 – 20754 = - 5606

Дата добавления: 2015-08-17