
Читайте также:
|
Тема: Статистики и параметры распределения
2.1. Вычисление статистик различными способами:
Таблица 2.1
Расчет статистик методом произведений
| Середины классов (центральные значения) Xi | Частоты ni | Xi *ni | Xi2 | Xi2 * ni |
| ИТОГО | Σ=75 | Σ=2491 | Σ=87531 |
Среднее арифметическое:
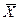 =
= 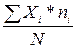 =
= 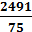 = 33,21 см
= 33,21 см
Дисперсия:
D = 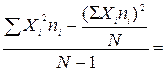
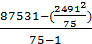
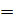 64,81
64,81 
Среднеквадратическое отклонение:
σ = 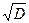 = √64,81 = 8,05 см
= √64,81 = 8,05 см
Коэффициент вариации:
СV= 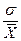 100%=
100%= 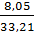 ∙ 100% = 0,24 ∙ 100% = 24% - это большое варьирование.
∙ 100% = 0,24 ∙ 100% = 24% - это большое варьирование.
Таблица 2.2
Расчет статистик методом условной средней
A (центральное значение класса, имеющий наибольшую частоту) = 37
| Середины классов (центральные значения классов) Xi | Частоты ni | Отклонения Ai=Xi -А | Ai*ni | Ai 2* ni |
| -16 | -144 | |||
| -12 | -144 | |||
| -8 | -72 | |||
| -4 | -44 | |||
| Σ=333 | Σ=-284 | Σ=5872 |
Среднее значение:
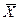 = A+
= A+ 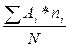 = 37 +
= 37 + 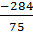 = 33,21 см
= 33,21 см
Дисперсия:
D = 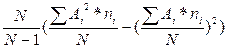 =
= 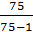 (
(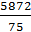 – (
– (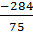
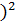 = 1,01 ∙ (78,29 – 14,33)=64,81 см2
= 1,01 ∙ (78,29 – 14,33)=64,81 см2
Среднеквадратическое отклонение:
σ = 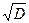 = √64,81 = 8,05 см
= √64,81 = 8,05 см
Коэффициент вариации:
CV= 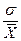 100%=
100%= 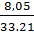 ∙ 100% = 0,24 ∙ 100% = 24 % - это большое варьирование.
∙ 100% = 0,24 ∙ 100% = 24 % - это большое варьирование.
Вычисление начальных моментов
Таблица 2.3
Определение сумм произведений условных произвольных отклонений различной степени на частоту классов
A (центральное значение класса, имеющий наибольшую частоту) =37
РасчетAi = 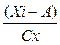 ;
; 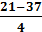 = - 4- неименованная величина
= - 4- неименованная величина
| Середины классов (центральные значения) Xi | Частоты ni | Условные произвольные отклонения | ||||||
| Ai | Aini | Ai2ni | Ai3ni | Ai4ni | (Ai+1) | (Ai+1)4ni | ||
| -4 | -36 | -576 | -3 | |||||
| -3 | -36 | -324 | -2 | |||||
| -2 | -18 | -72 | -1 | |||||
| -1 | -11 | -11 | ||||||
| Итого | Σ=75 | Σ=-71 | Σ=367 | Σ=-803 | Σ=3967 | Σ=2748 |
Система начальных моментов:
m1= 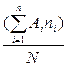 =
= 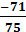 = -0,946
= -0,946
m2= 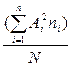 =
= 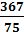 = 4,893
= 4,893
m3= 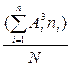 =
= 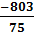 = -10,706
= -10,706
m4= 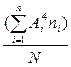 =
= 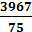 = 52,893
= 52,893
Проверка:
1. m4*= 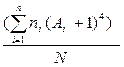 =
= 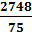 = 36,64
= 36,64
2. m4*= 4m1+ 6m2+4m3 +m4+1= 4 ∙ (-0,946) + 6 ∙ (4,893) + 4 ∙ (-10,706) + 52,893 + 1 = 36.64
Система центральных моментов:
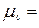 1;
1;
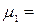 0;
0;
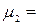 m2 – m12= 4.893-(-0,946
m2 – m12= 4.893-(-0,946 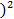 = 3.99
= 3.99
 m3 – 3m2 m1+ 2m13= -10.706 – 3 ∙ 4.893∙ (- 0.946) +2∙ (- 0. 946
m3 – 3m2 m1+ 2m13= -10.706 – 3 ∙ 4.893∙ (- 0.946) +2∙ (- 0. 946 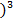 = 1.48
= 1.48
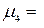 m4–4 m1m3+ 6 m12m2–3m14=52.893 - 4∙ (-0.946) ∙ (-10.706)+6∙ (-0.946
m4–4 m1m3+ 6 m12m2–3m14=52.893 - 4∙ (-0.946) ∙ (-10.706)+6∙ (-0.946 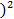 ∙4.893-3∙ (-0.946
∙4.893-3∙ (-0.946 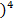 = 36.25
= 36.25
D = 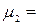 3.99
3.99
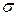 =
= 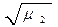 = √3.99 = 1.99
= √3.99 = 1.99
Для перехода к именованным величинам необходимо значения дисперсии D и среднеквадратического отклонения 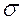 домножить на величину интервала Cx:
домножить на величину интервала Cx:
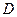 р= Сx2 *
р= Сx2 * 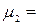
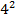 ∙ 3.99 = 63.84
∙ 3.99 = 63.84
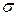 р=
р= 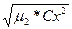 =
=  = √63.84 = 7.98
= √63.84 = 7.98
Система основных моментов:
(в расчетах используем неименованные величины)
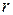 3= 3= 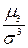 = = 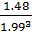 = 0.187 = 0.187
| 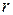 4= 4= 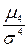 = = 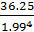 = 2.311 = 2.311
|
Среднее арифметическое:
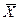 =A+m1Cх = 37 + (-0.946)*4 = 33.216
=A+m1Cх = 37 + (-0.946)*4 = 33.216
Коэффициент асимметрии (оценить результат):
Sk= 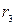 = 0.187 – асимметрия умеренная
= 0.187 – асимметрия умеренная
Коэффициент эксцесса (оценить результат):
E = 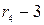 = 2.311-3 = -0.689 - эксцесс слабый
= 2.311-3 = -0.689 - эксцесс слабый
Основные ошибки статистик изучаемой величины ____:
(в расчетах используем именованные величины)
Ошибка среднего m 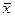 =
= 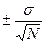 = ±
= ± 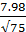 =± 0.92
=± 0.92
Ошибка среднеквадратического отклонения m 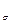 =
= 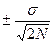 =± 0.008
=± 0.008
Ошибка коэффициента вариации mcv = ± 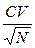
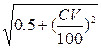 = ±
= ± 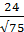 √0.5+(
√0.5+(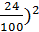 =± 2.06
=± 2.06
Ошибка коэффициента асимметрии mSk = ± 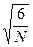 = ± 0.282
= ± 0.282
Ошибка коэффициента эксцесса mSe = ± 2* mSk = ± 0.564
Точность опыта P = 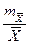 *100%=
*100%= 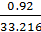 ∙ 100% = 2.76 %
∙ 100% = 2.76 %
Таблица 2.4
2.4.Сводная ведомость статистик по всем показателям:
| Наименование статистики | Показатели |
| D, см | |
| 2.4.1. Статистики ряда расположения: | |
| среднее арифметическое () | 33.21 |
| мода () | |
| медиана () | |
| 2.4.2. Статистики изменчивости | |
| дисперсия () | 64,81 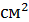
|
| среднеквадратичное отклонение () | 8.05 |
| коэффициент вариации () | 24 % |
| размах вариации () | |
| 2.4.3. Статистики отклонения ряда распределения от симметричного | |
| коэффициент асимметрии () | 0.187 |
| коэффициент эксцесса () | -0.689 |
| 2.4.4.Основные ошибки статистик | |
| ошибка среднего () | =± 0.92 |
| ошибка среднеквадратичного отклонения () | ± 0.008 |
| ошибка коэффициента вариации () | ± 2.06 |
| ошибка коэффициента асимметрии () | ± 0.282 |
| ошибка коэффициента эксцесса () | ± 0.564 |
| точность опыта () | 2.76 % |
Вывод: Рассчитал статистику для исследуемого признака различными способами: произведений, средней условной и момента. Так же вычислил основные ошибки и достоверности статистик, точности опыта.
Дата добавления: 2015-08-17; просмотров: 68 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Санкт – Петербург | | | Новини видавництва |