Натуральные, целые, рациональные и действительные числа

Числа - натуральные, целые (положительные и отри­цательные), рациональные и иррациональные, - со­ставляют множество действительных чисел.

Натуральные числа получаются путем последовательного прибавления 1, начиная с 1.

Действительное число а называется рациональ­ным, если существуют такие целые числа . В противном случае а называется иррациональным.

Множество рациональных чисел обозначается Q.

Каждое действительное число может быть записано в виде десятичной дроби. При этом рациональным числам и только им соответствуют периодические десятичные дроби. Однако, например, разложение в десятичную дробь действительного числа 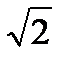, т. е. такого однозначно определенного положительного действительного числа, квадрат которого равен 2, не является периодическим. Таким образом, 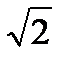— иррациональное число. Мно­жество рациональных чисел бесконечно и счетно, а множество иррациональных чисел несчетно.

Дата добавления: 2015-08-20