Пересечение множеств

Пересечением множеств А и В называется множество С, состоящее из элементов, которые принадлежат как множеству А, так и множеству В одновременно. Объединение множеств А и В обозначается через АÇВ. Таким образом,

С=АÇВ={cïcÎA и сÎВ}.

Т.е. пересечение множеств есть общая часть данных множеств.

Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АÇВ={2, 4}. Если А – множество отличников группы, а В – множество юношей, то АÇВ составляет множество юношей-отличников.

По аналогии с алгеброй чисел пересечение называют произведением множеств.

С помощью кругов Эйлера пересечение множеств А и В изображается следующим образом (заштрихованная часть на рис. 2.2.).

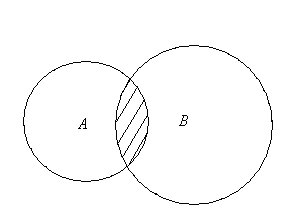
Рис. 2.2

Операцию «пересечение» можно аналогичным образом распространить и на n множеств , , …, . Множество С= Ç Ç…Ç – это множество, состоящее из элементов, которые принадлежат одновременно всем множествам , , …, .

Рассмотрим такой пример. Если А – множество отличников группы, а В – множество неуспевающих студентов, то АÇВ – пустое множество.

Если АÇВ=Æ, то множества А и В называются непересекающимися (Рис. 2.3).

Рис. 2.3

В противном случае, т.е. если АÇВ¹Æ, множества А и В пересекаются.

Операция пересечения множеств обладает многими свойствами операция умножения чисел:

АÇВ = ВÇА – коммутативность (переместительность);

(АÇВ)ÇС = АÇ(ВÇС) – ассоциативность (сочетательность);

(АÈВ) ÇС = (АÇС) È (ВÇС) – дистрибутивность (распределительность).

Укажем такие свойства операции пересечения множеств, которыми операция умножения чисел не обладает:

АÇА=А – идемпотентность;

Если АÍВ, то АÇВ=А. Например, если А={2, 4}, а В={2, 4, 6, 7}, то АÇВ={2, 4}. Если А – множество отличников группы, а В – все множество студентов группы, то АÇВ – множество отличников группы. Данная ситуация представлена на рис.2.4. с помощью кругов Эйлера.

Рис. 2.4

Дата добавления: 2015-08-20