
Читайте также:
|
В отличие от объединения и пересечения множеств эта операция определяется только для двух множеств. Разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат множеству А, но не входят в множество В. Разность множеств А и В обозначается через А\В. Таким образом,
С=А\В={cïcÎA и сÏВ}.
Например, если А={1, 2, 3, 4, 5}, а В={2, 4}, то А\В={1, 3, 5}. Если А – множество отличников группы, а В – множество юношей, то А\В составляет множество девушек-отличников.
С помощью кругов Эйлера для случаев, изображенных на рис.2.5, разность множеств А и В изображается следующим образом (заштрихованная часть).
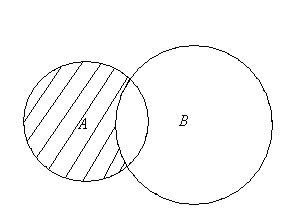
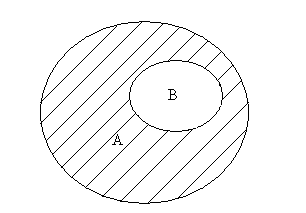
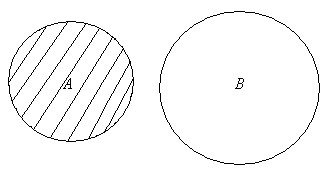
Рис. 2.5
Заметим, что разность множеств не является ни коммутативной, ни ассоциативной операцией.
Дата добавления: 2015-08-20; просмотров: 103 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пересечение множеств | | | Симметрическая разность множеств |