Симметрическая разность множеств

Симметрической разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат какому-то одному из множеств А или В. Симметрическая разность множеств А и В обозначается через АDВ.

С=АDВ= (А\В)È (В\А).

Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АDВ={1, 3, 5, 6, 7}. Если А – множество отличников группы, а В – множество юношей, то А\В составляет множество девушек-отличников и юношей-неотличников.

С помощью кругов Эйлера симметрическая разность множеств А и В АDВ изображается следующим образом (заштрихованная часть на рис. 2.6).

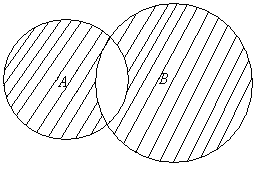
Рис. 2.6

В отличие от разности множеств симметрическая разность является коммутативной, ассоциативной и дистрибутивной операцией:

АDВ = ВDА – коммутативность (переместительность);

(АDВ)DС = АD(ВDС) – ассоциативность (сочетательность);

(АDВ)ÇС = (АÇС) D (ВÇС) – дистрибутивность (распределительность).

Дата добавления: 2015-08-20