Реакция кодера на импульсное возмущение

Мы можем описать кодер через его импульсную характеристику, т.е. в виде отклика кодера на единичный проходящий бит. Рассмотрим содержимое регистра (рис. 8.3) при прохождении через него двоичной единицы.

Содержимое регистра кодера и формирование выходной последовательности при входной последовательности 1 0 0 … представляется следующей таблицей:

Предположим теперь, что вектор сообщения m = 1 0 1 закодирован с использовани­ем сверточного кода и кодера, показанного на рис. 8.3. Введены три бита сообще­ния, по одному в момент времени t₁,t₂ и t₃, как показано на рис. 8.4. Затем для очистки регистра в моменты времени t₄ и t₅ введены (К - 1) = 2 нуля, что в результа­те приводит к смещению конечного участка на всю длину регистра. Последователь­ность на выходе выглядит следующим образом: 1 1 1 0 0 0 1 0 1 1, где

крайний левый символ представляет первую передачу. Для декодирования сообщения нужна полная последовательность на выходе (включающая кодовые символы). Для удаления со­общения из кодера требуется на единицу меньше нулей, чем имеется разрядов в регистре, или К - 1 очищенных бит.

В момент времени t₆ показан нулевой выход, это должно дать читателю возможность убедиться в том, что в момент времени t₅ регистр устанавливается в исходное состояние. Таким образом, в момент времени t₆ уже можно передавать новое сообщение.

Последовательность на выходе при единице на входе называется откликом кодера на импульсное возмущение, или его импульсной характеристикой. Для входной последо­вательности m = 1 0 1 данные на выходе могут быть найдены путем суперпозиции или линейного сложения смещенных во времени входных "импульсов".

Обратим внимание на то, что эти данные на выходе такие же, как и на рис. 8.4, что указывает на линейность сверточных кодов — точно так же как и в блочных кодах. Название сверточный кодер (convolutional encoder) возникло именно вследст­вие этого свойства генерации данных на выходе кодера с помощью линейного сложения (или свертки) смещенных во времени импульсов входной последовательности m с импульс­ной характеристикой кодера. Сверточные коды и сверточные кодеры описываются с помощью порождающей мат­рицы сверточного кода бесконечного порядка:

G = ,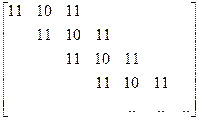

в которой строки являются импульсной характеристикой и ее циклическими сдвигами. Пустые ячейки в представленной матрице G заполнены нулями. Выходная последовательность u вычисляется по порождающей матрице G и входной последовательности m по правилам умножения матриц

u = m G.

Данное выражение является матричной формой процедуры дискретной свертки.

---

Дата добавления: 2015-08-02