Полиномиальное представление

Связи кодера описываются с помощью порождающего многочлена (генератора), аналогичного используемому для описания реализации обратной связи регистра сдвига циклических кодов. Сверточный кодер можно представить в виде набора из п порождающих многочленов, по одному для каждого из п суммато­ров по модулю 2. Каждый многочлен имеет степень К - 1 или меньше и описывает связь кодирующего регистра сдвига с соответствующим сумматором по модулю 2. Коэффициенты возле каждого слагаемого равны либо 1, либо 0, в зависимости от того, имеется ли связь между регистром сдвига и сумматором по модулю 2. Для кодера на рис 8.3 можно записать порождающий многочлен g₁ (X) для верхних связей и g₂(X) — для нижних:

g₁(X) = 1 + X + X²,

g₂(X) = 1 + X².

Здесь слагаемое самого нижнего порядка в полиноме соответствует входному разряду регистра. Выходная последовательность находится следующим образом:

U(X) = m(X)g₁(X) чередуется с m(X)g₂(X)

Прежде всего, выразим вектор сообщения m = 1 0 1 в виде многочлена, т.е. т(Х) = 1 + X². Для очистки регистра мы снова будем предполагать использование нулей, следующих за битами сообщения. Тогда выходящий многочлен U(X), или выходящая последова­тельность U кодера (рис. 8.3) для входного сообщения m может быть найдена сле­дующим образом:

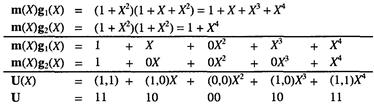В этом примере мы начали обсуждение с того, что сверточный кодер можно тракто­вать как набор регистров сдвига циклического кода. Мы представили кодер в виде порождающих многочленов, с помощью которых описываются циклические коды. Однако мы пришли к той же последовательности на

выходе, что и на рис. 8.4, и к той же, что и в предыдущем разделе, полученной при описании реакции на импульсное возмуще­ние.

Дата добавления: 2015-08-02