Представление состояния и диаграмма состояний

Сверточный кодер принадлежит классу устройств, известных как конечный авто­мат (finite-state machine). Это общее название дано системам, обладающим памя­тью о прошедших сигналах. Прилагательное конечный показывает, что существует ограниченное число состояний, которое может возникнуть в системе. Что имеется в виду под состоянием (state) в системах с конечным его числом? В более общем смысле состояние включает наименьшее количество информации, на основе ко­торой вместе с текущими входными данными можно определить данные на выхо­де системы. Состояние дает некоторое представление о прошлых событиях (сигналах) и об ограниченном наборе возможных выходных данных в будущем. Будущие состояния ограничиваются прошлыми состояниями. Для сверточного кода со степенью кодирования 1/n состояние представлено содержимым К - 1 крайних правых разрядов (рис. 8.4). Знание состояния плюс знание следующих данных на входе является необходимым и достаточным условием для определения данных на выходе. Итак, пусть состояние кодера в момент времени t_i определяет­ся как Х_i = т_i- 1, т_i - 2, ..., т_i - К + 1. i-я ветвь кодовых слов U_i полностью опре­деляется состоянием X_i и введенными в настоящее время битами т_i; таким образом, состояние X_i описывает предысторию кодера для определения данных на его выходе. Состояния кодера считаются Марковскими в том смысле, что вероятность Р(Х_i + 1 │ Х_i,,..., Х₀) нахождения в состоянии X_i + 1, определяемая всеми предыду­щими состояниями, зависит только от самого последнего состояния Х_i, т.е. она равна Р(Х_i + 1 │ Х_i).

Одним из способов представления простых кодирующих устройств является диаграмма состояния (state diagram); такое представление кодера, изображенного на рис. 8.3, показано на рис. 8.5. Состояния, показанные в рамках диаграммы, представляют собой возможное содержимое К - 1 крайних правых разрядов реги­стра, а пути между состояниями — кодовые слова ветвей на выходе, являющиеся результатом переходов между такими состояниями. Состояния регистра выбраны следующими: а =00, b = 10, с = 01 и d =11; диаграмма, показанная на рис. 8.5, иллюстрирует все возможные смены состояний для кодера, показанного на рис. 8.3. Существует всего два исходящих из каждого состояния перехода, соот­ветствующие двум возможным входным битам. Для каждого пути между со­стояниями записано кодовое слово на выходе, связанное с переходами между со­стояниями. При изображении путей, сплошной линией принято обозначать путь, связанный с нулевым входным битом, а пунктирной линией — путь, связанный с единичным входным битом. Отметим, что за один переход невозможно перейти из данного состояния в любое произвольное. Так как за единицу времени перемеща­ется только один бит, существует только два возможных перехода между состоя­ниями, в которые регистр может переходить за время прохождения каждого бита. Например, если состояние кодера — 00, при следующем смещении возможно воз­никновение только состояний 00 или 10.

Пример 8.1. Сверточное кодирование

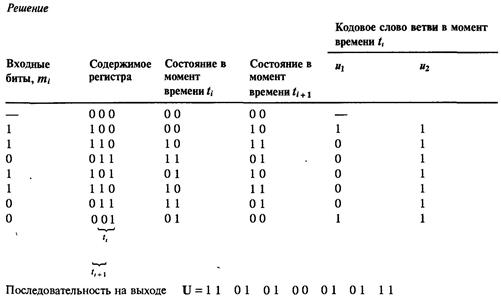
Для кодера, показанного на рис. 8.3, найдите изменение состояний и результирующую по­следовательность кодовых слов U для последовательности сообщений m=1 1 0 1 1, за кото­рой следует К — 1 = 2 нуля для очистки регистра. Предполагается, что в исходном состоянии регистр содержит одни нули.

Пример 8.2. Сверточное кодирование (продолжение примера 8.1)

В примере 8.1 исходное содержимое регистра — все нули. Это эквивалентно тому, что дан­ной последовательности на входе предшествовали два нулевых бита (кодирование является функцией настоящих информационных бит и К — 1 предыдущих бит). Повторите задание примера 8.1, предполагая, что данной последовательности предшествовали два единичных бита, и убедитесь, что теперь последовательность кодовых слов U для входной последова­тельности m = 1 1 0 1 1 отличается от последовательности, найденной в примере 8.1.

Сравнивая эти результаты с результатами из примера 8.1, можно видеть, что каждое кодовое слово выходной последовательности U является функцией не только входного бита, но и предыдущихК - 1 бит.

---

Дата добавления: 2015-08-02