К некоторым термодинамическим процессам

Рассмотрим теперь какой-нибудь термодинамический процесс, подчиняющийся уравнению 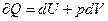(1)

(1)

1) Изохорный процесс (V=const)

Если объем системы постоянен, то второй член в правой части данного уравнения равен 0 и работа расширения равна 0. Но для такого процесса уравнение (1) примет вид:

;

Из полученного результата следует два вывода:

1. изменение внутренней энергии численно равно тепловому эффекту изохорного процесса

2. тепловой эффект изохорного процесса определяется только исходным и конечным состояниями процесса и не зависит от пути его протекания.

2) Изобарный процесс (р=const)

Запишем (1) для этого процесса

U+pV=H – энтальпия (теплосодержание) - функция обладает всеми свойствами функции состояния

1) аддитивная функция, так как внутренняя энергия U и объем V характеризуются свойствами аддитивности при р=const

2) любое приращение этой функции обладает свойствами полного дифференциала, следовательно изменение данной функции определяется исходным и конечным состояниями системы и не зависит от пути перехода из исходного в конечное состояние

Как видим:

1) изменение энтальпии характеризует величину теплового эффекта изобарного процесса

2) тепловой эффект изобарного процесса определяется только исходным и конечным состояниями системы и не зависит от пути перехода из исходного в конечное состояние

Работа расширения изобарного процесса равна

dA=pdV

A=p(V₂-V₁)=pΔV

Для идеального газа в соответствии с уравнением Менделеева-Клапейрона

A=R(n₂T₂-n₁T₁)

Если процесс протекает при p=const и T=const, то Т₂=Т₁ и A=(n₂-n₁)RT=ΔnRT

3) Изотермический процесс (Т=const)

Выберем в качестве системы один моль идеального газа, тогда (1) примет вид:

p=RT/V

dQ=dA=RTdlnV

4) Адиабатный процесс – процесс, который осуществляется в изолированной системе, т.е. без теплообмена с окружающей средой. В этом случае (1) примет вид:

, так как Q=const

dA=-dU

A=U₁-U₂=-ΔU (работа совершается за счет убыли внутренней энергии)

Если в качестве системы взят 1 моль идеального газа, то

dA=-c_VdT

A=c_V(T₁-T₂)

Поставим теперь задачу получить уравнение состояния идеального газа в изолированной системе – такое уравнение называется уравнением адиабаты.

1)

Подставим р и поделим на Т:

получим cVdlnT+RdlnV=0

так как R=cp-cv,

то dlnT+(γ-1)dlnV=0

где

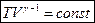(1)

2)

Q=const

cpdT-Vdp=0

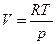
cpdlnT-Rdlnp=0

cpdlnT+(cv-cp)dlnp=0

γdlnT+(1-γ)dlnp=0

(2)

(3)

Термохимия

Наука о тепловых эффектах химических реакций.

Закон Гесса как следствие из I-го начала термодинамики

(1841год) Сумма тепловых эффектов одного ряда последовательно протекающих реакций равна сумме тепловых эффектов другого ряда последовательно протекающих реакций, если исходные и конечные вещества этих двух рядов одинаковы, а все процессы осуществляются при р, Т=const ил и V,T=const.

Можно показать, что закон Гесса является прямым следствием из I-го закона т/д. В самом деле, как было показано ранее, для процессов при постоянном объеме или при постоянном давлении и неизменной температуре тепловые эффекты реакций определяются только исходным и конечным состояниями системы и не зависят от пути процесса. Из закона Гесса вытекает несколько следствий. Рассмотрим два важнейших из них.

1. Тепловой эффект химической реакции равен сумме теплот образования продуктов за вычетом суммы теплот образования исходных веществ с учетом стехиометрических коэффициентов.

Теплотой образования вещества называется тепловой эффект химической реакции синтеза одного моль вещества из простых веществ. Теплоты образования простых веществ равны нулю.

Пример: С₂Н₂

2С+H₂=C₂H₂+ΔН_обр.

Уравнение химической реакции с включением в него теплового эффекта этой реакции называется термохимическим уравнением.

В соответствии с законом Гесса термохимические уравнения обладают свойствами обычных алгебраических уравнений. Их можно почленно складывать друг с другом и вычитать.

Покажем, что сформулированное следствие действительно вытекает из закона Гесса. Рассмотрим в качестве примера следующую химическую реакцию:

C₂H₂+2H₂=C₂H₆+ΔH

Запишем уравнения для теплот образования веществ участников данной реакции:

2C+H₂=C₂H₂+ ΔH_C2H2 (1)

2C+3H₂=C₂H₆+ ΔH_C2H6 (2)

Вычтем (1) из (2):

Получим C₂H₂+2H₂=C₂H₆+ΔH, где ΔH=ΔH_C2H6-ΔH_C2H2

Теплоты образования важнейших веществ в стандартных условиях (р=1атм, t=298K) приведены в справочниках.

2. Тепловой эффект химической реакции равен сумме теплот сгорания исходных веществ за вычетом суммы те6плот сгорания продуктов реакции с учетом стехиометрических коэффициентов.

Теплотой сгорания вещества называется тепловой эффект реакции полного окисления 1 моль вещества молекулярным кислородом. Продуктами сгорания углеводородов являются CO₂ и H₂O. Теплоты сгорания CO₂ и H₂O принимаются равными нулю.

Пример:

C₂H₂+2H₂=C₂H₆+ΔH

C₂H₂+5/2O₂=2CO₂+H₂O+ΔH_{сгор.С2Н2} (3)

H₂+1/2O₂=H₂O+ ΔH_сгор.Н2 (4)

C₂H₆+7/2O₂=2CO₂+3H₂O+ΔH_{сгор.С2Н6} (5)

Преобразуем уравнения (5)-[(3)+(4)]:

C₂H₂+2H₂=C₂H₆+ ΔH

где ΔH= ΔH_{сгор.С2Н2}+2 ΔH_сгор.Н2- ΔH_{сгор.С2Н6}

---

Дата добавления: 2015-08-10