Читайте также:
|
Закон Дюлонга и Пти – атомная теплоемкость твердого тела равна ~25Дж/моль·К.
Закон Коппа-Неймана – теплоемкость твердого кристаллического вещества аддитивно складывается из величин атомных теплоемкостей.
В 1904 годе А.Эйнштейн предложил квантовую теорию теплоемкости твердого кристаллического вещества. Основные допущения теории:
1. Все атомы твердого кристаллического вещества представляют собой гармонические осцилляторы.
2. Частоты колебаний всех атомов твердого кристаллического тела одинаковы.
В соответствии с теорией Эйнштейна существует статистическое распределение всех молекул твердого тела по энергиям. Оно подчиняется закону Больцмана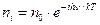 
,
где ni – число молекул, находящихся на i-том энергетическом уровне колебательного движения
n0 – число молекул на нулевом уровне колебательного движения
i - колебательное квантовое число (i=1,2,3…)
h – постоянная Планка
k – постоянная Больцмана
ν – частота колебаний
Т – абсолютная температура
Используя формулу Больцмана можно рассчитать число молекул на I-ом энергетическом уровне, на II-ом, на III-ем…
, 
, …
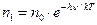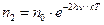Для одного грамм-атома кристаллического вещества
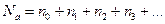- число Авогадро
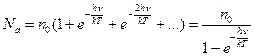
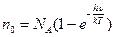
Внутренняя энергия, приходящаяся на 1 степень свободы UT, будет равна:
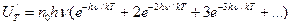
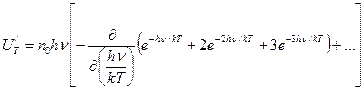
После преобразования получим
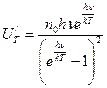
Подставим вместо n0 его значение:
Получим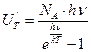 
Продифференцируем по Т:
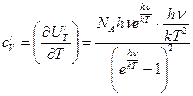
Обозначим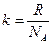 
- постоянная Больцмана
- характеристическая температура
Тогда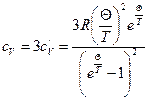 
- уравнение Эйнштейна
Проанализируем полученное уравнение:
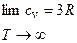Если R=8,31кДж·г·атом, то 3R≈25 кДж·г·атом, что хорошо согласуется с законом Дюлонга-Пти.
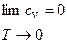
Закон Дюлонга-Пти справедлив только для области высоких температур.
Дебай усовершенствовал теорию Эйнштейна распределения атомов твердого тела по частотам колебания. При этом Дебай допустил, что распределение по частотам колебания в твердом веществе подобно спектру колеблющейся струны.
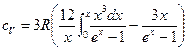- уравнение Дебая
где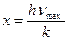 
Дата добавления: 2015-08-10; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теплоемкость идеального газа | | | Теплоемкость жидкостей |