Как термодинамическая функция состояния

Докажем, что внутренняя энергия является т/д функцией системы. Внутренняя энергия согласно определению является аддитивной функцией.

U=E_пост.+Е_кол.+Е_вр.+Е_эл.+…

Докажем теперь, что изменение внутренней энергии определяется только конечным и начальным состояниями ее и не зависит от пути протекания процесса. Рассмотрим пример:

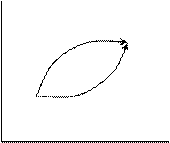V

ΔU₁ 2

ΔU₂

T

Докажем, что в любом случае ΔU₁ = ΔU₂

Доказательство: от противного

ΔU₁ ≠ ΔU₂

1) пусть ΔU₁ > ΔU₂

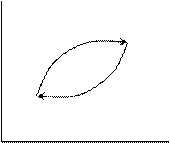V

ΔU₁ 2

-ΔU₂

T

Тогда осуществим между 1 и 2 цикл. В результате осуществления такого цикла мы будем получать выигрыш ΔU₁ - ΔU₂ > 0 за счет внутренней энергии системы и осуществив этот цикл сколь угодно большое число раз мы можем получить большой выигрыш в энергии. Но это не возможно, так как противоречит I-му закону термодинамики.

2) пусть ΔU₂ > ΔU₁

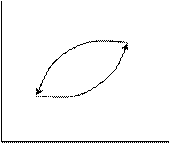V

-ΔU₁ 2

ΔU₂

T

Это также не возможно.

Поэтому ΔU₁ = ΔU₂, а внутренняя энергия является термодинамической функцией состояния системы.

Анализ уравнения I-го закона термодинамики

Запишем уравнение I-го закона т/д для случая, когда единственной работой процесса является работа расширения, т.е. δQ=dU+pdV (1)

1) пусть внутренняя энергия системы – функция объема и температуры U=U(V,T).

Тогда 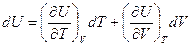(2)

(2) в (1)

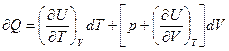(3)

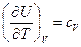калорические коэффициенты

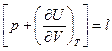
Тогда 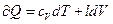(4)

Чтобы выявить их физический смысл, проведем анализ (4):

V=const 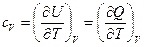- изохорная теплоемкость системы

Т=const 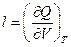- величина показывает значение теплового эффекта при изменении объема системы на единицу при Т=const.

Для идеального газа в соответствии с законом Джоуля внутренняя энергия является функцией температуры и не зависит ни от объема, ни от давления газа. Поэтому 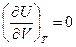и 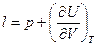, l=p – для идеального газа.

Таким образом, .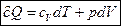

2) пусть теперь внутренняя энергия является функцией давления и температуры U=U(р,T).

Так как 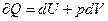(5)

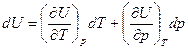Тогда (6)

При V=V(p,T) 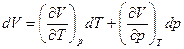(7)

Подставим теперь (6) и (7) в (5):

получим 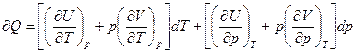(8)

Введем обозначение:

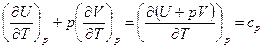- изобарная теплоемкость

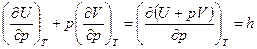- коэффициент показывает, какое количество теплоты надо сообщить системе, чтобы изменить (увеличить) ее давление на 1.

Тогда .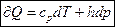

Для идеального газа в соответствии с законом Джоуля .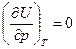

Тогда 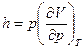(9)

Для 1 моль идеального газ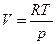а , а 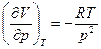. Подставим (9) в (10):

получим .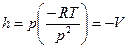

Таким образом .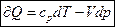

Установим взаимосвязь между теплоемкостями c_p и c_V. Воспользуемся для этого уравнением I-го закона термодинамики (уравнение (1)). Применим это уравнение к изобарному процессу:

Получим .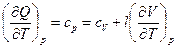

Для идеального газа l=p, а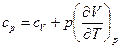

Для 1 моль идеального газа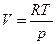

; .

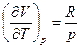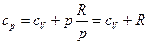Теплоемкость при постоянном давлении всегда больше чем при постоянном объеме c_p=c_V+R.

Дата добавления: 2015-08-10