Теплоемкость жидкостей

На данный момент отсутствуют общие методы расчета теплоемкости жидких веществ. Для выражения температурной зависимости жидкостей используется уравнение

c_p=a+bT+cT²+c^//T²

(значения а, b, c, c^/ табл.)

Истинная теплоемкость – теплоемкость для данной температуры.

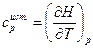
Если разделить переменные, то получим

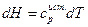
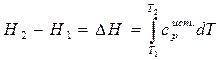
Разделим левую и правую части уравнения на (Т₂-Т₁), получим

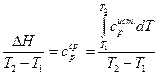
где 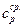- средняя теплоемкость.

Средняя теплоемкость – количество тепла необходимое для нагревания вещества от Т₁ до Т₂.

II-ой закон термодинамики

Он запрещает создание двигателей, которые осуществляли бы работу за счет тепловой энергии окружающих предметов без разности температур, то есть он запрещает создание вечных двигателей II-го рода. Существует несколько формулировок (постулатов) II-го закона т/д.

I постулат Оствальда: Невозможно построить вечный двигатель II-го рода.

II постулат Клаузиуса: Никакая совокупность процесса не может приводить к самопроизвольному переходу тепла от холодного тела к горячему, тогда как самопроизвольный переход тепла от горячего тела к холодному может быть единственным результатом процесса.

III постулат Томпсона: Никакая совокупность процесса не может приводить к полному превращению теплоты в работу, тогда как превращение работы в теплоту может быть единственным результатом процесса.

II закон термодинамики решает вопрос о направлении протекания самопроизвольных процессов в термодинамических системах, поэтому этот закон имеет различное математическое выражение для обратимых и необратимых процессов.

Математическое выражение II-го закона термодинамики

для обратимых процессов

Предположим, что протекает какой-либо обратимый процесс в идеальном газе.

Принцип Каратеодори: В непосредственной близости от любого т/д состояния системы существуют такие состояния, которые недостижимы адиабатным путем (без теплообмена с окружающей средой).

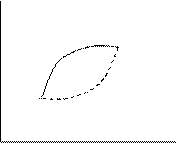
Рассмотрим систему – идеальный газ.

p

ΔU 2

1 -ΔU

T

1 – исходное состояние

Сообщим системе количество тепла Q. В результате этого система перейдет в состояние 2. В соответствии с принципом Каратеодори невозможно вернуться в состояние 1 из 2 адиабатным путем (без теплообмена с окружающей средой). Этот принцип является прямым следствием из II-го закона термодинамики. Для доказательства воспользуемся принципом от противного. Предположим, что из 2 в 1 можно вернуться адиабатным путем. Запишем уравнение I-го закона т/д последовательно для прямой и и обратной стадий циклического процесса.

Для прямой стадии Q=ΔU+A₁ (1)

Для обратной стадии 0=-ΔU+A₂ (2)

где А₂ – работа предполагаемого адиабатного процесса.

Сложим почленно (1) и (2):

Q=A₁+A₂

Получили, что при осуществлении циклического процесса вся теплота, сообщенная системе, превращена в работу, но это не возможно, так как противоречит II-му закону т/д в формулировке Томпсона. Следовательно, наше предположение не верно и принцип Каратеодори справедлив. Из принципа Каратеодори вытекает как следствие, что теплота не является функцией состояния системы, но существует какая-то функция состояния связанная с теплотой (S=f(T)).

Убедимся в этом на примере обратимого процесса, протекающего в идеальном газе. Запишем математическое выражение I-го закона термодинамики для данного процесса в следующей форме:

δQ=c_VdT+pdV (1)

Тогда учитывая, что для 1 моль идеального газа получим

δQ=c_VdT+RTdlnV (2)

Q=f(T,lnV)

Из математики если z=f(x,y) и δz=Mdx+Ndy,

то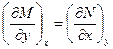

При 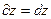, т.е. z- полный дифференциал

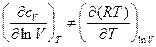
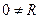
Данное равенство не соблюдается, следовательно, δQ не является полным дифференциалом, а теплота не является функцией состояния системы. Поделим левую и правую части уравнения (2) на Т:

Тогда 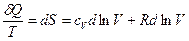(3)

dS обладает свойствами полного дифференциала, поскольку перекрестные производные одинаковы:

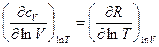
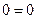
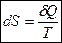(4)

Функция S обладает всеми свойствами функции состояния – это энтропия.

Поэтому важнейшим выводом из II-го закона т/д является вывод о существовании энтропии как термодинамической функции состояния, а уравнение (4) представляет собой математическое выражение II-го закона т/д для обратимых процессов в идеальном газе.

Докажем теперь, что уравнение (4) справедливо для любых обратимых процессов, протекающих в любых т/д системах. Рассмотрим для этого систему, состоящую из 2-х частей:

1 2

Пусть 1 представляет идеальный газ, а вторая часть произвольное вещество. Пусть система находится в состоянии термодинамического равновесия (Т=const). Пусть без нарушения равновесия бесконечно-малое количество δQ₁ теплоты переходит от части 1 к 2. Тогда вторая часть системы получит точно такое же количество тепла δQ₂.

δQ₁=-δQ₂

,

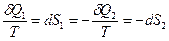
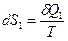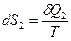
Уравнение (4) справедливо для любых т/д процессов в любых т/д системах.

Математическое выражение II-го закона термодинамики

для необратимых процессов

Предположим, что между одними и теми же исходными и конечными состояниями системы осуществляется какой-либо т/д процесс сначала обратимо, а затем необратимо. Запишем уравнение I-го закона т/д для обратимого и необратимого процессов.

δQ_обр.=dU+δA_обр. (1)

δQ_необр.=dU+δA_необр. (2)

Вычтем почленно (2) из (1):

δQ_обр.- δQ_необр.= δA_обр.- δA_необр. (3)

Проанализируем полученное выражение:

Разности в левой и правой частях уравнения (3) могут быть =0, >0 и <0.

1) рассмотрим первый случай, когда =0:

δQ_обр.- δQ_необр.=0, δA_обр.- δA_необр. =0

Но эти равенства невозможны, так как теплота и работа не являются функциями состояния системы.

Следовательно, δQ_обр.- δQ_необр.≠0, δA_обр.- δA_необр. ≠0

2) второй случай

δQ_обр.- δQ_необр.>0, δA_обр.- δA_необр. >0

В термодинамике положительной считается теплота, переходящая от окружающей среды к системе. Следовательно, выражение (3) будет иметь следующий физический смысл:

Вся теплота, сообщенная системе превращена в работу, но это невозможно, так как противоречит II-му закону т/д в формулировке Томпсона. Предположение неверно.

3) третий случай

δQ_обр.- δQ_необр.<0, δA_обр.- δA_необр. <0

Выражение (3) имеет физический смысл:

Вся работа, совершенная системой, превращена в теплоту, но но это вполне возможно, так как не противоречит II-му закону т/д в формулировке Томпсона.

Следовательно, δQ_обр.>δQ_необр.

>

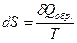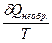
dS> 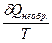(4)

Неравенство (4) – это математическое выражение II-го закона т/д для необратимых процессов.

δA_обр.> δA_необр. A_обр.>A_необр.

А_обр.=А_max

Поэтому работу обратимого процесса будем называть максимальной работой процесса. Очень часто математическое выражение II-го закона термодинамики для обратимого и необратимого процессов объединяют в одно выражение, имея в виду, что знак > - для необратимого процесса, а знак = - для обратимого.

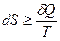(5)

Применение II-го закона термодинамики

к анализу процессов в изолированных системах

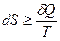Q=const → dS≥0 - выражение II-го закона термодинамики для адиабатного процесса.

Знак > - для необратимого процесса, характеризует протекание процессов в изолированной системе

Знак = - условие т/д равновесия в изолированной системе

Условием протекания является возрастание энтропии dS>0 (ΔS>0).

При установившемся равновесии энтропия максимальна dS=0 (d²S<0).

На основе данного вывода немецкий ученый Клаузиус сформулировал свой постулат:

Энтропия Вселенной непрерывно возрастает и при достижении max энтропии наступит тепловая смерть Вселенной. Но этот постулат не верен, так как Вселенная не является изолированной системой и к ней эти выводы не применимы.

Дата добавления: 2015-08-10