
|
Читайте также: |
Q1 – количество теплоты, сообщенное рабочему телу при Т1 от теплоисточника.
Q2 – количество теплоты, отданное рабочим телом при Т2 холодильнику.
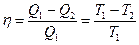 - КПД тепловой машины при работе по циклу Карно не зависит от природы рабочего тела (идеальный газ, пар, воздух и др.), а определяется только интервалом температур, в котором совершается работа.
- КПД тепловой машины при работе по циклу Карно не зависит от природы рабочего тела (идеальный газ, пар, воздух и др.), а определяется только интервалом температур, в котором совершается работа.
P T1
1
Q1=A1
-A4=ΔU 2
4 A2=-ΔU
-A3=-Q2 3
T2
V
Термодинамические потенциалы и направление протекания
самопроизвольных процессов в термодинамических системах
Термодинамическим потенциалом называется такая т/д функция состояния системы, по изменению которой в т/д процессах можно определять их максимальную работу. Изменение т/д потенциалов характеризует условия т/д равновесия.
В термодинамике чаще всего используются 4 т/д функции-потенциала. Для их изучения воспользуемся объединенным математическим выражением I-го и II-го законов т/д в нескольких формах (в восьми).
Так как 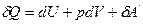
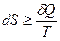
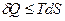
То  (1)
(1)
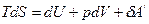 - для обратимого процесса (2)
- для обратимого процесса (2)
Пусть А/=0 (только процесс расширения)
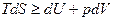 (3)
(3)
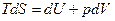 (4)
(4)
Так как H=U+pV
U=H-pV
dU=dH-pdV-Vdp
то  (5)
(5)
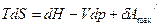 (6)
(6)
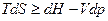 (7)
(7)
 (8)
(8)
Проанализируем теперь выражения 1-8 для некоторых т/д процессов.
1. изохорно-изоэнтропийный процесс
V, S=const
1) пусть этот процесс протекает при условии А/=0, тогда применяя к этому процессу (3) получим dU≤0 – знак неравенства характеризует самопроизвольный необратимый процесс.
 dU<0 (1)
dU<0 (1)
ΔU<0
Для обратимого – ΔU=0.
Выражения (1) представляют собой условие самопроизвольного протекания изохорно-изоэнтропийного процесса. Таким условием является убыль внутренней энергии системы. При установившемся равновесии внутренняя энергия имеет минимальное значение.
 dU=0 - условие минимума функции (2)
dU=0 - условие минимума функции (2)
d2U>0
3) используем теперь уравнение (2)
При V,S=const будет:
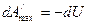
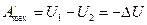
Как видим, внутренняя энергия является изохорно-изоэнтропийным термодинамическим потенциалом.
2. изобарно-изоэнтропийный процесс
р, S=const
1) если А/=0, то применим (7)
dH≤0 – для самопроизвольного необратимого процесса.
 dH<0
dH<0
ΔН<0
Как видим, условием самопроизвольного протекания этого процесса является убыль энтальпии системы. Равновесие в системе при р, S=const наступает, когда энтальпия ее минимальна.
 dH=0 - условие т/д равновесия в системе при р, S=const
dH=0 - условие т/д равновесия в системе при р, S=const
d2H>0
2) применим (6), получим
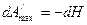
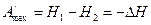
Как видим, убыль энтальпии характеризует его максимальную работу. Поэтому энтальпия является изобарно-изоэнтропийным термодинамическим потенциалом.
Изохорно-изоэнтропийный и изобарно-изоэнтропийный процессы на практике осуществляются крайне редко, поэтому примеры 1) и 2) имеют больше теоретическое, чем практическое значение. Чаще всего осуществляются изохорно-изотермические и изобарно-изотермические процессы.
3) Изохорно-изотермический процесс
V, T=const
1) Пусть А/=0, тогда применим (3)
dU-TdS≤0
dU-d(T·S)≤0
d(U-TS)≤0
U-TS=F – обладает свойствами функции состояния (так как бесконечно малое приращение обладает свойствами полного дифференциала) – свободная энергия Гельмгольца, изохорно-изотермический потенциал.
 dF=0 - условие т/д равновесия в системе при V, T =const
dF=0 - условие т/д равновесия в системе при V, T =const
d2F>0
2) применим (2), которое будет иметь вид:
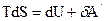
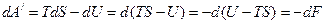
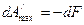
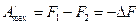
Как видим, убыль энергии Гельмгольца равна максимальной работе изохорно-изотермического процесса.
Таким образом, энергия Гельмгольца является изохорно-изотермическим т/д потенциалом.
Установим теперь взаимосвязь F с другими т/д функциями и параметрами системы.
F=U-TS (9)
U=F=TS
F – свободная энергия
TS – связанная энергия – та часть энергии, которая не может быть превращена в работу.
Продифференцируем (9) и подставим в него (4):
dF=dU-TdS-SdT=dU-dU-pdV-SdT=-SdT-pdV
dF=-SdT-pdV
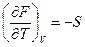 ;
; 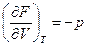
Запишем теперь уравнение (9) последовательно для исходного и конечного состояний системы в каком-либо изохорно-изотермическом процессе:
F1=U1-TS1
F2=U2-TS2
Вычтем почленно второе уравнение из первого:
F2-F1=(U2-U1)-T(S2-S1)
ΔF=ΔU-TΔS - уравнение Гиббса-Гельмгольца (10)
ΔF<0 →
ΔF>0 ←
ΔF=0 ↔


F2-F1=ΔF=-A/max
Перепишем (10) в следующей форме:
 - уравнение Гиббса-Гельмгольца для максимальной работы
- уравнение Гиббса-Гельмгольца для максимальной работы
4) Изобарно-изотермический процесс
p, T=const
1) Применим (7) для А/=0
dH-TdS≤0
dH-dTS≤0
d(H-TS)≤0
H-TS=G – функция состояния – свободная энергия Гиббса или энергия Гиббса, изобарно-изотермический потенциал.
dG≤0 – знак “–“ характеризует условие самопроизвольного протекания изобарно-изотермического процесса. Таким условием является убыль энергии Гиббса термодинамической системы при p, T=const.
При установившемся равновесии энергия Гиббса системы минимальна.
 dG=0 условие минимума
dG=0 условие минимума
d2G>0
2) Если изобарно-изотермический процесс протекает обратимо, то из уравнения (6) будем иметь:
dA/max=TdS-dH=-d(H-TS)=-dG
A/max=G1-G2=-ΔG
Как видим, убыль энергии Гиббса характеризует максимальную работу изобарно-изотермического процесса. Таким образом, энергия Гиббса является изобарно-изотермическим т/д потенциалом.
Установим взаимосвязь энергии Гиббса с другими т/д функциями и параметрами состояния системы:
G=H-TS (11)
H=U+pV
G=U+pV-TS
G=F+pV - взаимосвязь энергий Гиббса и Гельмгольца (12)
dG=dF+pdV+Vdp
dF=-SdT-pdV
dG=-SdT+Vdp (13)
Проанализируем (13):
 ;
; 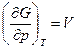
Запишем теперь последовательно уравнение (11) для исходного и конечного состояний системы в изобарно-изотермическом процессе:
G1=H1-TS1
G2=H2-TS2
G2-G1=H2-H1-T(S2-S1) (14)
ΔG=ΔH-TΔS уравнение Гиббса-Гельмгольца
С помощью этого уравнения можно рассчитать изменение энергии Гиббса для термодинамических процессов:
ΔG<0 →
ΔG>0 ←
ΔG=0 ↔
Подставим в (11) следующие выражения:

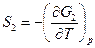
ΔG=-A/max
Получим уравнение max работы Гиббса-Гельмгольца
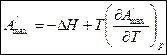
Энергия Гиббса и энергия Гельмгольца идеального газа
Дата добавления: 2015-08-10; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Изменение энтропии в разных процессах | | | Изменение энергии Гельмгольца при смешении идеальных газов |