Автомат Мили.

Как было указано выше рекуррентные соотношения

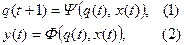
где q(t), q(t + 1) Q, x(t) X, y(t) Y, дополненные начальным условием q(1) = q₀, задают оператор T, который преобразует всякую конечную последовательность входящих символов

x = x(1) x(2)...x(r) в некоторую последовательность выходных символов

y = Tx = y(1) y(2).... y(r).

Автомат называется конечным, еслиего внутренний алфави т конечен. Каждый конечный автомат может быть представлен двумя конечными таблицами с двойным входом, соответствующими функциям Ψ и Φ. В этих таблицах, которые называются соответственно матрицей переходов и матрицей выходов, строки занумерованы входными буквами, а столбцы состояниями.

П р и м е р.

Пусть Q = {1, 2, 3}, X ={a, b}, Y = {a, b, c}. Φ, Ψ заданы таблицами 1 и 2.

Команды данного автомата будут иметь вид:

1) 1а→3b, 2) 1b→2c, 3)2a→3a, 4)2b→3c, 5)3a→1b, 6) 3b→3c.

Таблица 1 Таблица 2.

Ψ(q, x) Φ(q, x)

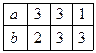
Пусть в некоторый момент времени t автомат находится в состоянии 1 и на вход его в моменты t, t + 1, t + 2 подается последовательность abb, тогда автомат перерабатывает ее в выходную последовательность bcc, и в момент t + 3 будет находиться в состоянии 3.

Комбинаторика.

Комбинаторикой называется область математики, в которой изучаются способы подсчета числа элементов в конечных множествах. Комбинаторика имеет широкий круг приложений (теория вероятностей, теория информации и, наконец, математический анализ).

Определение.

Допустим имеем множество А, состоящее из n элементов. Будем составлять из элементов этого множества различные группы, содержащие по m элементов каждой группе. Такие группы называются соединениями.

Комбинаторика выясняет, сколько соединений из n элементов по m, удовлетворяющих тем или иным условиям, можно составить.

Дата добавления: 2015-07-20