Машина Тьюринга.

Работа алгоритма производится на некотором устройстве реализации, содержащем процессор для выполнения операций, внешнюю и внутреннюю память для хранения, поиска и изменения данных.

Одним из методов представления алгоритмов является машина Тьюринга (МТ), которая включает в себя следующие элементы.

Бесконечную в обе стороны ленту, разделенную на ячейки В каждой ячейке может быть записан один из символов рабочего алфавит а машины 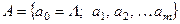.Любой алфавит должен содержать пустой символa₀ = Λ< запись которого означает отсутствие информации в данной ячейке. Совокупность символов алфавита, записанных на ленте, называется словом.

Считающее - записывающее устройство (СЗУ).

СЗУ представляет собой головку, которая обладает способностью обозревать текущую ячейку ленты, считывать букву, записанную в ячейке, записывать на место считанной любую другую из алфавита А (возможно ту же самую), а также передвигаться по ленте накаждом шаге на одну ячейку вправо или влево.

Управляющее устройство (УУ).

УУ руководит действиями СЗУ в соответствии с программой Р. При этомУУ может находиться в одном из состояний Q = {q₁, q₂,... q_n, q₀ }, среди которых должно быть обязательно выделено начальное состояние q₁ и заключительное состояние q₀. Действия УУ зависит от входящих в программу команд, от текущего состояния УУ и от символа, записанного в обозреваемой в данный момент ячейке. Будем считать, что это крайняя левая непустая ячейка.

Программа Р.

Программа состоит из множества команд, на основании которых УУ определяет действия головки СЗУ на каждом шаге работы машины. Т. к. действия машины Тьюринга на каждом шаге определяются символом, записанным в обозреваемой ячейке и состоянием УУ, то команды программы имеют следующий вид

где q, r 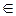Q, a, b A.

Программа через УУ сообщает, что должна делать СЗУ в случае, если состояние УУ равно q 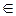Q (q ≠ q₀), и в обозреваемой ячейке записан символ а А. УУ находит команду с левой частью qa и действует следующим образом,

а) если правая часть этой команды равна br, то М записывает в обозреваемую ячейку b, и УУ переходит в состояние r;

b) если правая часть этой команды равна bRr или bLr, то М записывает в обозреваемую ячейку b, головка сдвигается на одну ячейку вправо или влево соответственно, и УУ переходит в состояние r.

Формально, машина Тьюринга – это тройка М = (А, Q, P), где:

А – алфавит машины (т.е. символы, которые записываются в ячейки, включая пустой символ а₀ = Λ);

Q – конечное множество состояний УУ, содержащее два выделенных элемента q₁ и q₀;

Р – множество команд УУ, которое называется программой машины.

Если машина, начав работу с исходным словом, на некотором шаге придет в заключительное состояние, то она называется применимой к этому слову, а полученное слово результатом применения машины Тьюринга к исходному слову. Если же машина ни в какой момент времени не придет в заключительное состояние, то она называется неприменимой к данному слову, и результат ее работы неопределенен.

П р и м е р 1.

Применима ли машина Тьюринга М, заданная программой Р, к слову S? Если применима, то найти результат применения машины Тьюринга к данному слову.

где верхняя строка – это записанное на ленте слово, нижняя строка показывает, какая в данный момент ячейка обозревается, и в каком состоянии находится УУ.

Найдем результат применения машины к слову S.

В начальный момент, как видно из таблицы, СЗУ обозревает символ 1 и УУ находится в состоянии q₁. Находим в программе команду с левой частью q₁1. Это команда 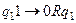Она означает, что в рассматриваемую ячейку записывается 0, головка сдвигается на одну ячейку вправо, и УУ устанавливается в состояние q₁. В результате применения этой команды имеем:

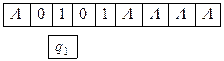
Снова обозревается символ 1 и УУ находится в состоянии q₁. В обозреваемую ячейку записывается 0, головка сдвигается на одну ячейку вправо и остается в состоянии q₁. Получим

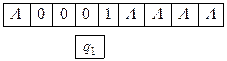
В этот раз обозревается символ 0 и УУ находится в состоянии q₁. Соответствующая команда в программе имеет вид q₁0 → 1Rq₁, поэтому в обозреваемую ячейку записывается 1, головка сдвигается на одну ячейку вправо, и УУ остается в состоянии q₁.

На следующем шаге обозревается символ 1 и УУ находится в состоянии q₁. выполняется команда

q₁1 → 0Rq₁:

Далее обозревается пустая ячейка Λ, и УУ находится в состоянии q₁. Соответствующая команда имеет вид q₁Λ → ΛLq₂:

Далее, согласно программе, головка движется влево вдоль всего слова, не изменяя записанные в ячейках символы до тех пор, пока не примет следующее положение

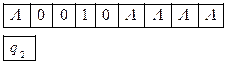
В этом случае соответствующая команда имеет вид q₂Λ → ΛRq₀. Это означает, что обозреваемая ячейка остается пустой, головка сдвигается вправо и переходит в состояние q₀.

Состояние q₀ – заключительное, поэтому машина заканчивает работу, т.е. машина применима к слову S. Чтобы узнать результат применения, рассмотрим непустые символы на ленте, которые мы получили. Увидим, что слово S преобразовано в слово S′ = 0010.

Заметим, что данная программа реализует процесс инвертирования заданного слова т.е. замену единиц на нули, а нулей на единицы. Программа составлена таким образом, что в заключительном состоянии СЗУ обозревает первый символ полученного слова, т.е. возвращается в исходное положение.

Программу машины можно задать таблично.

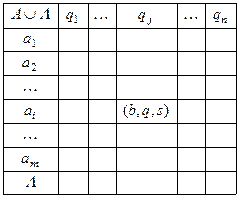
П р и м е р 2.

Построить машину Тьюринга, удваивающую натуральные числа, записанные в унарной системе счисления.

Расширим исходный алфавит А ={ | } до А′ ={ |, α }. искомую машину построим в алфавите А′ {Λ}. Программа машины будет выглядеть так

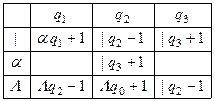
При работе машина считывает букву в обозреваемой ячейке и находит клетку в таблице, соответствующую считанной букве (|, α, Λ) и состоянию машины (q_i). ± сдвиг головки соответственно вправо или влево.

Применим машину к слову | |.

1)

2)

3)

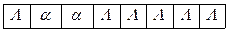
4)

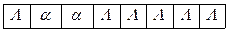
5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

Состояние q₀ – заключительное, поэтому машина заканчивает работу.

Введение новой буквы α и замена исходных | на α позволяет различать исходные | и новые (приписанные). Состояние q₁ обеспечивает замену | на α, состояние q₂ обеспечивает поиск α, предназначенных для замены на |, и останов машины, если α не обнаружено, q₃ обеспечивает дописывание | в случае, когда произошла замена α на |.

Существуют следующие стандартные машины Тьюринга.

1. Тождественная машина Е – применима к любому слову u над алфавитом А и E(u) = u.

2. Пусть А - алфавит и ▲А (▲ – неподвижный ограничитель), n 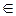N. Копирующей машиной К_n называется машина, применимая к любому слову u 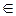A, причем

K_n (u) = u▲, u▲,.... u▲.

n – раз

3. Пусть А – алфавит и (α. β) 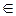А (α ≠ β). Машиной, заменяющейα на β, называется машина З_α←β, применимая к любому слову u, так что

З_α←β(u) =

Теорема. Тождественная. копирующая и заменяющая машины существуют.

---

Дата добавления: 2015-07-20