Читайте также:
|
Таблица производных:
Таблица производных:
Доказательство:
Дифференциал функции.
Определение: Если Х независимая переменная, то дифференциал функции f(x) наз. f’(x)Dx=u обозначают df(x).
Теорема об инвариантной форме первого дифференциала.
df(x)=f’(x)dx
Доказательство:
1).
2). 
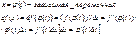
Дата добавления: 2015-07-25; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Правила дифференцирования | | | Производная высших порядков. |