
Читайте также:
|
Опред: точка x0 называется точкой max (min) если существ. такая окрестность данной точки, что в x0 фун. принимает наибольшее (наименьшее) значение.
Точка х0 наз. точкой экстремума, если эта точка max или min данной функции.

Теорема: Необходимый признак экстремума функции.
Если х0 точка экстремума f(x), то:
1). Либо не существует f’(x0)
2). Либо f’(x0)=0
Док-во:
1). Не сущест. f’(x0)
2). Сущест. f’(x0) - по т. Ферма f’(x0)=0

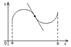
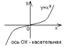
Замечание: данные условия не являются достаточными.
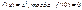
Дата добавления: 2015-07-25; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Производные степенных и тригонометрических функций. | | | Поиск наибольшего и наименьшего значения непрерывных функций на замкнутом промежутке. |