Читайте также:
|
Теорема: Если f(x) и g(x) дифферен. в точке х, то: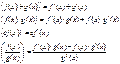 
Доказательство 2-го правила.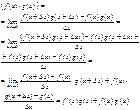 
Теорема о произв. сложной функции.
Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).
Доказательство:
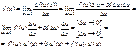
Рассмотрим f(x) в задан. промеж.: [a,b].
g(y): [f(a),f(b)] – наз. обратной к f(x), если g(f(x))=x, для любого " X Î[a,b]
f(g(y))=y, для любого у Î[f(a),f(b)]
y=sin x [-p/2, p/2], тогда
x=arcsin y, yÎ[1,1]
sin arcsin y = y;
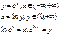arcsin * sin x=x
Дата добавления: 2015-07-25; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Физический смысл производной. | | | Теорема о произв. обратной функции. |