
Читайте также:
|
Основные формулы: 
Производная сложной функции.

Производные показательных и логарифмических функций.
Основные формулы:

Если z=z(x) – дифференцируемая функция от x, то формулы имеют вид:

Производные обратных тригонометрических функций.
Основные формулы: 
Для сложных функций:
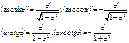
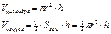
Дата добавления: 2015-07-25; просмотров: 68 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формула Тейлора. | | | Признаки экстремума функций. |