Лабораторгая работа № 3. Принципы цифровой фильтрации

Одной из основных задач цифровой обработки сигналов является их фильтрация, при которой осуществляется селекция требуемых полезных составляющих сигнала и подавление других мешающих его компонент и шумов. Подобные операции над сигналами выполняют цифровые фильтры (ЦФ). Цифровым фильтром называют цифровое вычислительное устройство, преобразующее последовательность числовых отсчетов 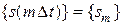входного сигнала в последовательность числовых отсчетов 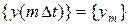выходного сигнала (здесь 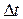− интервал дискретизации). Если через 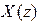и 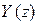обозначить z-преобразования входных и выходных сигналов, то системной функцией ЦФ называется функция

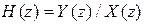. (1)

Частотный коэффициент передачи ЦФ может быть выражен через системную функцию как

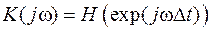. (2)

Цифровые фильтры делятся на два больших класса: нерекурсивные и рекурсивные. В нерекурсивных (или трансверсальных) ЦФ отклик зависит только от значений входной последовательности. Такие фильтры обрабатывают входной дискретный сигнал в соответствии с алгоритмом

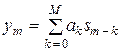, (3)

где 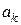− «весовые» коэффициенты, 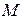− порядок фильтра, т. е. максимальное число запоминаемых чисел. Для трансверсального фильтра системная функция в соответствии с (1), (3) имеет вид

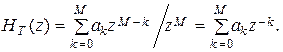(4)

Рекурсивные ЦФ отличаются от нерекурсивных тем, что для формирования -го выходного отсчета используются предыдущие значения не только входного, но и выходного сигналов:

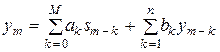. (5)

Здесь коэффициенты 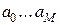характеризуют нерекурсивную часть, а коэффициенты 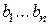− рекурсивную часть алгоритма цифровой фильтрации. Из (1), (5) получаем выражения для системной функции рекурсивного ЦФ:

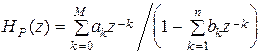. (6)

Важное практическое значение имеют методы синтеза ЦФ, обеспечивающие заранее заданные свойства, например, требуемый вид импульсной или частотной характеристик. Наиболее часто задача синтеза понимается в том смысле, что требуется создать ЦФ, эквивалентный данному аналоговому прототипу. При этом выходные отсчеты ЦФ с гарантированной точностью должны совпадать с дискретными значениями выходного сигнала гипотетического аналогового фильтра-прототипа. Наиболее простыми методами синтеза являются метод инвариантных импульсных характеристик и метод инвариантных частотных характеристик, которые и будут рассмотрены далее в лабораторной работе.

В качестве аналоговых фильтров прототипов будут рассмотрены фильтры нижних частот (ФНЧ) различного порядка. А именно, будут рассматриваться два наиболее известных типа передаточных функций таких фильтров – Баттерворта и Чебышева. В дальнейшем предполагается, что все характеристики таких фильтров являются нормированными, т. е. их коэффициент передачи в полосе пропускания равен 1 (0 dB), а частота среза – 1 рад/сек. Фильтры Баттерворта (с максимально плоской характеристикой) отличаются наибольшей равномерностью АЧХ как в полосе пропускания, так и в полосе подавления. У АЧХ полностью отсутствуют пульсации (максимумы и минимумы). Однако в результате ухудшается линейность фазовой характеристики. Фильтр Чебышева (фильтр равных пульсаций) характеризуется крутым спадом АЧХ и немонотонностью коэффициента передачи в полосе пропускания. Такие фильтры также обладают нелинейной фазовой характеристикой. Ниже в таблицах Таб.1 – Таб.3 приведены передаточные функции фильтров Баттерворта и Чебышева до пятого порядка включительно. Передаточные функции этих фильтров представлены в виде 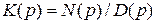, где полиномы и 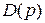определены в соответствующих таблицах.

Таб.1 (Фильтры Баттерворта)

Порядок n
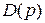
		p +1

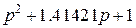
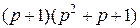
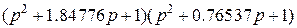
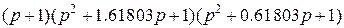
Таб.2. (Фильтры Чебышева-1, пульсации в полосе пропускания 1 dB)

Порядок n
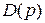
	1.965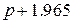
	0.983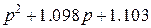
	0.491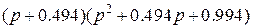
	0.246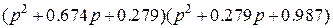
	0.123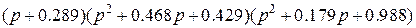

Таб.3 (Фильтры Чебышева-2, пульсации в полосе пропускания 0.5 dB)

Порядок n
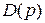
	2.863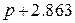
	1.431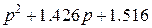
	0.716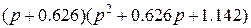
	0.358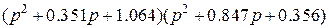
	0.1789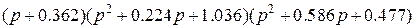

Целью настоящей лабораторной работы является изучение методов синтеза линейных цифровых фильтров на примере ФНЧ различных порядков.

Работа выполняется на ЭВМ с использованием программной среды Maxima.

Дата добавления: 2015-07-20