Пример выполнения задания 1. В качестве примера рассмотрим сигнал вида

В качестве примера рассмотрим сигнал вида

Вводим в компьютер исходные данные:

kill(all)$

numer:true$ ratprint:false$

s0:2.3$ t0:0.014$ K:128$

s(t):=s0/(1+(t/t0)^2)^2$

Вычислим граничные значения сигнала T 1 и T 2, задаваясь критерием, в соответствии с которым в этих точках значения сигнала уменьшаются до значения 0.01 от максимального значения . Для вычисления верхней границы 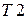набираем:

T2:find_root(s(t)/s(0)-0.01, t, t0, 20*t0)$

Так как − четная функция времени, то длительность сигнала может быть найдена следующим образом: T2 = T1, = T2 –T1.

Строим график . Для этого набираем:

tK:makelist(k*2*T2/K-T2,k,0,K-1)$

sK:map(s,tK),numer$

wxplot2d([discrete,tK,sK]);

Вычислим теперь амплитудно-частотный спектр (АЧС) 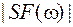сигнала . Для этого набираем:

N:K$

SF(w):=2*quad_qawo(s(t),t,0,T2,w,cos,'epsabs=1d-2)[1]$

SF0:SF(0),numer$

SFF(w):=SF(w)/SF0$

wN:makelist((n-N/2)/T2,n,0,N-1)$

SFN:makelist(SFF(wN[n+1]),n,0,N-1),numer$

wxplot2d([discrete,wN,SFN]);

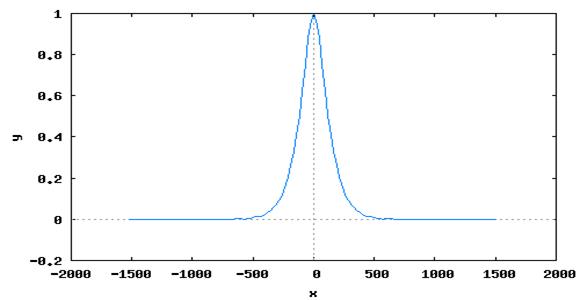
Здесь на последнем рис. для наглядности изображен нормированный на максимум амплитудно-частотный спектр исследуемого сигнала.

Для нахождения максимальной частоты 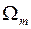в спектре сигнала будем использовать критерий, в соответствии с которым в точке 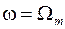значение модуля спектра 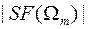уменьшается до значения 0.01 от максимального значения . Для вычисления 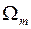набираем:

Wm:find_root(SF(w)/SF0-0.01, w, 1/T2, 50/T2);

491.9008154654611

Интервал дискретизации в соответствии с теоремой Котельникова

Dt:%pi/Wm;

0.0063866384336384

Для графического представления совокупности дискретных отсчетов 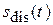набираем:

vmin:ceiling(-T2/Dt)-1$ vmax:ceiling(T2/Dt)$

tKK:makelist(k2*Dt,k2,vmin,vmax)$

sKK:map(s,tKK),numer$

wxplot2d([[discrete,tK,sK],[discrete,tKK,sKK]], [style,[lines],[impulses,2,1]]);

Используя последний график, предложить процедуру расчета максимальной частоты 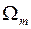в спектре сигнала .Показать, что это значение совпадает с ранее найденным.

Представим аналоговый сигнал рядом Котельникова. С этой целью набираем:

sink(t):=(if abs(t)<0.0001 then 1 else sin(t)/t)$

SK(t1):=sum(s(k2*Dt)*sink(Wm*(t1-k2*Dt)), k2,vmin,vmax)$

SKK:map(SK,tK),numer$

Выведем на одном рисунке графические зависимости аналогового сигнала и его представление рядом Котельникова:

wxplot2d([SK(t1),[discrete,tK,sK]],[t1,-T2,T2]);

Убеждаемся в совпадении полученных графических зависимостей и и, следовательно, в возможности представления сигнала в произвольный момент времени рядом Котельникова.

---

Дата добавления: 2015-07-20