Дискретное представление аналоговых сигналов

В связи с интенсивным развитием цифровых методов передачи, приема и обработки аналоговых сигналов возникает необходимость их представления в дискретной или цифровой формах, например, совокупностью дискретных отсчетов 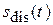(Рис. 5):

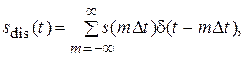(1)

где 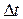− интервал дискретизации (интервал времени между соседними отсчетами); 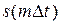− значения функции в моменты времени 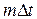; 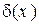− дельта-функция.

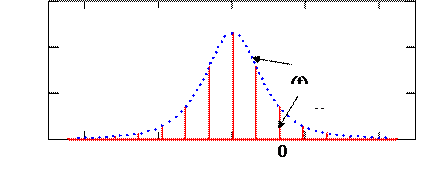
Рис. 5

Дискретное представление реализуется на основе теоремы Котельникова:

если наибольшая частота в спектре аналогового сигнала не превышает значения 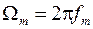, то сигнал во все моменты времени определяется последовательностью своих дискретных отсчетов (1), взятых через интервал времени .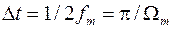

Аналоговый сигнал может быть определен с помощью совокупности дискретных отсчетов 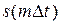рядом Котельникова

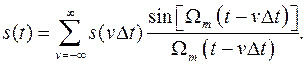(2)

Реально используемые сигналы имеют конечную длительность 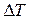. Спектры таких сигналов имеют теоретически бесконечную протяженность, т. е. 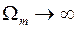. Однако такие сигналы могут быть представлены рядом Котельникова (2) приближенно, если при определении 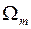отбросить «хвосты» функций спектров, начиная с 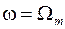. При этом количественные критерии, на основе которых производится ограничение протяженности спектра частотой 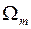, могут быть различными − по доле отбрасываемой с «хвостами» энергии сигнала относительно полной энергии, по величине спектра на частоте 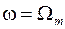относительно максимального значения и др. Для сигналов конечной длительности число дискретных отсчетов N в (1) конечно и равно

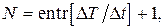(3)

где 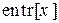− целая часть x.

2. Восстановление аналогового сигнала по совокупности дискретных отсчетов

Теоретически восстановление аналогового сигнала по совокупности дискретных отсчетов реализуется рядом Котельникова (2).

Возможность аппаратурного восстановления аналогового сигнала по дискретным отсчетам нетрудно понять, используя спектральное представление дискретного сигнала 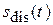(1). Известно [1, 2, 5], что спектр 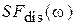совокупности отсчетов 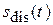(1) определяется выражением

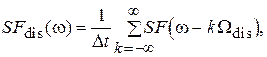(4)

где 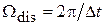− частота дискретизации аналогового сигнала; 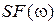− спектр аналогового сигнала , т.е. .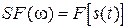

Из выражения (4) следует, что слагаемые суммы при 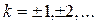представляют собой копии спектра 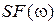, смещенные по оси частот вправо и влево на величину .

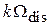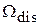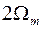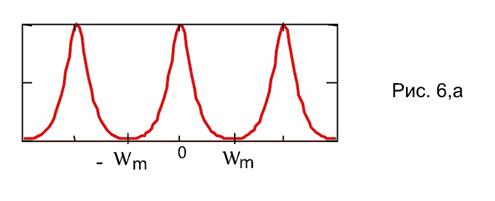
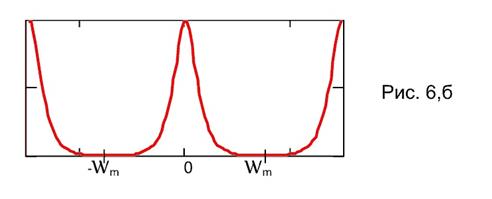
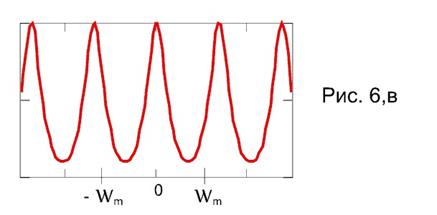
В зависимости от соотношения между величинами и спектр 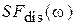(4) имеет различный характер (рис. 6. а, б, в).

cWm

Если 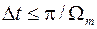(т. е. интервал дискретизации аналогового сигнала выбирается в соответствии с условиями теоремы Котельникова), то 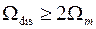и соседние копии спектра 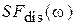в (4) сигнала не перекрываются; при 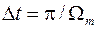(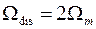) соседние копии примыкают друг к другу (рис. 6,а); при 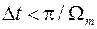(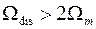) соседние копии спектра 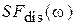разделены между собой конечными интервалами протяженностью 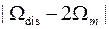, на которых значения спектра равны нулю (рис. 6,б).

Отсутствие перекрытия соседних копий спектра 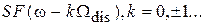позволяет выделить без искажений нулевую (k= 0) копию спектра 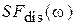из суммы в правой части (4) с помощью идеального фильтра нижних частот (ФНЧ), имеющего частотный коэффициент передачи

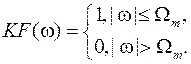(5)

Это значит, что при подаче на ФНЧ с 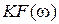(5) дискретного сигнала 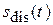на его выходе сформируется сигнал 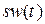, спектр которого определится выражением

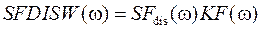(6)

и этот спектр идентичен спектру 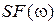восстанавливаемого сигнала . Отсюда вытекает, что сформированный на выходе ФНЧ временной сигнал 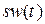со спектром 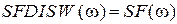идентичен исходному аналоговому сигналу: .

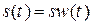Если 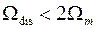(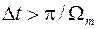), то соседние копии спектра 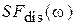перекрываются (рис. 6,в) и накладываются друг на друга, так что на частотном интервале 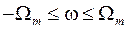спектр 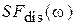не будет идентичен спектру 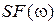сигнала . Следовательно, спектр 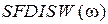на выходе ФНЧ, определяемый выражением (6), не будет совпадать со спектром 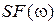и сформированный на выходе ФНЧ (5) сигнал 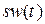не будет идентичен исходному аналоговому сигналу . Таким образом, если дискретизация аналогового сигнала не удовлетворяет условиям теоремы Котельникова (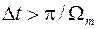), то восстановление аналогового сигнала по дискретным отсчетам без искажений невозможно.

Работа выполняется на ЭВМ с использованием программной среды Maxima.

Дата добавления: 2015-07-20