Пример выполнения задания 2

Обозначим 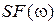− спектр аналогового сигнала ; 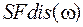− спектр дискретного сигнала 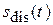. Ограничимся представлением на графике слагаемых суммы из (4) при 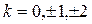. Учтем, что частота дискретизации 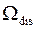связана с интервалом дискретизации соотношением 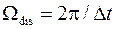. Тогда для вывода на экран графических зависимостей модулей этих спектров от частоты набираем

Wdis:2*%pi/Dt$

SFdis(w):=(1/Dt)*sum(SF(w-kk*Wdis),kk,-2,2)$

SFdis0:SFdis(0),numer$

SFDis(w):=SFdis(w)/SFdis0$

wN3:makelist((nw-N/2)*3000.0/N,nw,0,N-1)$

SFD:map(SFDis,wN3),numer$

SF3:map(SFF,wN3),numer$

wxplot2d([[discrete,wN3,SF3],[discrete,wN3,SFD]]);

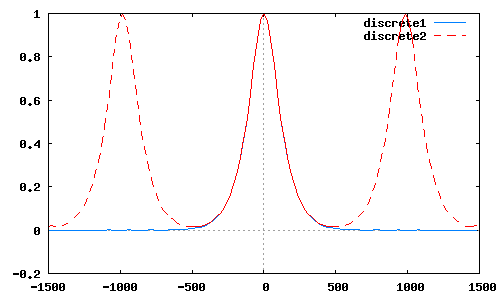
Здесь сплошной линией изображен нормированный амплитудно-частотный спектр (АЧС) исходного аналогового сигнала , а пунктиром − три периода АЧС дискретного сигнала 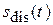. Убеждаемся, что амплитудные спектры 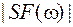и 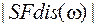на интервале частот 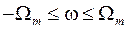идентичны. Поэтому для однозначного восстановления аналогового сигнала может быть использована часть спектра 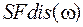(4) дискретного сигнала 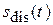(1), определенная в области частот .

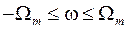Рассмотрим теперь прохождение дискретного сигнала 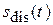через идеальный фильтр нижних частот с частотой среза, равной максимальной частоте в спектре сигнала . Частотный коэффициент передачи такого фильтра (5) запишется следующим образом:

h(x):=(if x<=0 then 0 else 1)$

KF1(w):=(h(w+Wm)-h(w-Wm))$

Спектральную плотность сигнала на выходе любого фильтра можно найти как произведение пектральной плотности входного сигнала на коэффициент передачи фильтра.

Сравним теперь спектральные плотности сигналов на выходе двух фильтров. Первый из которых является описанным выше идеальным фильтром нижних частот с частотным коэффициентом передачи (5). Второй фильтр представляет собой обычную RC -цепочку с такой же частотой среза, равной 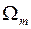(частоту среза будем определять по уровню 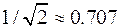от максимума). Известно [1−3], что частотный коэффициент передачи такого фильтра может быть записан в виде

KF2(w,tau):=1/(1+%i*w*tau)$

Здесь tau − постоянная времени фильтра. Ее значение найдем по заданной частоте среза:

tau0:find_root(cabs(KF2(Wm,tau))-0.707, tau, 0, 10/Wm),numer;

0.0020335441905483

Для сравнения изобразим на одном рисунке амплитудно-частотные характеристики (АЧХ) двух исследуемых фильтров:

wxplot2d([KF1(w),cabs(KF2(w,tau0))],[w,-1500,1500], [y,-0.1,1.1]);

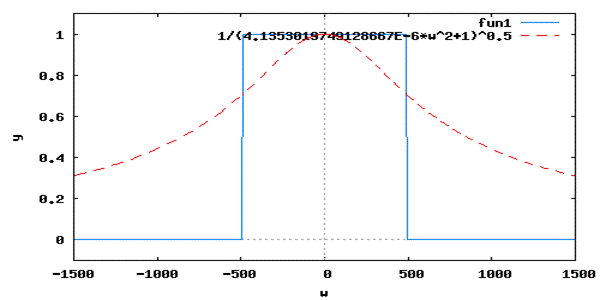
Изображаем на одном рис. зависимости от частоты следующих функций: нормированный на максимум амплитудно-частотный спектр (АЧС) сигнала на выходе идеального ФНЧ (сплошная кривая), нормированный на максимум АЧС сигнала на выходе RC -фильтра (пунктир) и нормированный на максимум АЧС исходного аналогового сигнала (штриховая кривая):

SF_1(w):=SFDis(w)*KF1(w)$

SF_1d:map(SF_1,wN3),numer$

SF_2(w):=cabs(SFDis(w)*KF2(w,tau0))$

SF_2d:map(SF_2,wN3),numer$

wxplot2d([[discrete,wN3,SF_1d],[discrete,wN3,SF_2d],

[discrete,wN3,SF3]]);

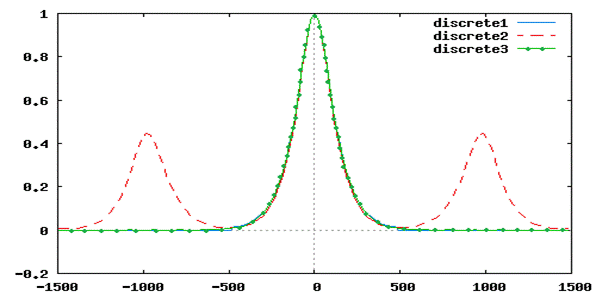
Из анализа этого рис. следует, что точное восстановление аналогового сигнала из дискретного возможно при условии, что фильтр обладает идеальной прямоугольной частотной характеристикой. Если же форма амплитудно-частотной характеристики фильтра отличается от прямоугольной, то это приводит к искажению спектра восстанавливаемого сигнала.

Подтвердим вышесказанное, вычислив сами сигналы (как функции времени) на выходах рассматриваемых двух фильтров. Для этого используем формулы обратного преобразования Фурье. Для этого набираем:

ass:makelist(realpart(sum(SF3[n] *exp(%i*tK[k]*wN3[n]),n,1,N)),k,1,K)$

asw1:makelist(realpart(sum(SF_1d[n]

*exp(%i*tK[k]*wN3[n]),n,1,N)),k,1,K)$

asw2:makelist(realpart(sum(SF_2d[n]

*exp(%i*tK[k]*wN3[n]),n,1,N)),k,1,K)$

Тогда графические зависимости сигналов, нормированных на свои максимальные значения, примут вид:

wxplot2d([[discrete,tK,asw1],[discrete,tK,asw2],

[discrete,tK,ass]]);

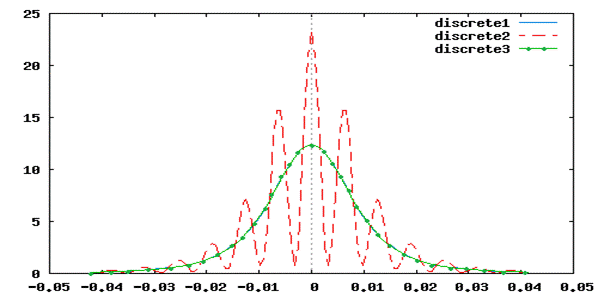
Из этого рис. также следует, что восстанавливаемый сигнал совпадает с исходным аналоговым сигналом только, если фильтр обладает идеальной прямоугольной частотной характеристикой. В противном случае (см. пунктир) восстанавливаемый сигнал имеет существенные отличия от исходного.

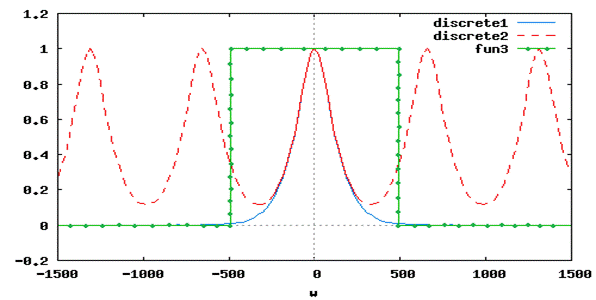
Рассмотрим теперь случай, когда интервал дискретизации 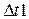аналогового сигнала в 1.5 раза больше максимального значения интервала дискретизации, определяемого теоремой Котельникова, т. е.

Dt1:1.5*Dt$ Wdis1:2*%pi/Dt1$

Найдем вначале спектр дискретного сигнала при выбранном интервале дискретизации. Для этого набираем:

SFdis1(w):=(1/Dt1)*sum(SF(w-kk*Wdis1),kk,-2,2)$

SFDis10:SFdis1(0)$

SFDis1(w):=SFdis1(w)/SFDis10$

SFD1:map(SFDis1,wN3),numer$

В результате нормированные на свои максимумы амплитудно-частотные спектры (АЧС) дискретного сигнала и исходного аналогового сигнала примут вид

wxplot2d([[discrete,wN3,SF3],[discrete,wN3,SFD1],

KF1(w)],[w,-1500,1500]);

Здесь сплошной линией изображен нормированный АЧС исходного аналогового сигнала; пунктиром − нормированный АЧС дискретного сигнала при 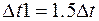и, наконец, линией с точками – АЧХ идеального ФНЧ. Убеждаемся в некотором отличии спектра 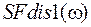в полосе пропускания ФНЧ 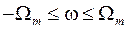от спектра 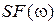исходного аналогового сигнала . Объяснить причину несовпадения спектров.

Определим теперь форму сигнала на выходе идеального ФНЧ, если на вход этого фильтра подавать дискретный сигнал со спектром 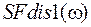, т. е. сигнал, полученный в результате дискретизации с шагом 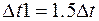. Для этого вначале вычислим спектральную плотность такого сигнала, а затем вычислим преобразование Фурье, используя формулу дискретного преобразования Фурье. В результате имеем

SF_3(w):=SFDis1(w)*KF1(w)$

SF_3d:map(SF_3,wN3),numer$

asw3:makelist(realpart(sum(SF_3d[n]

*exp(%i*tK[k]*wN3[n]),n,1,N)),k,1,K)$

wxplot2d([[discrete,tK,ass], [discrete,tK,asw3]]);

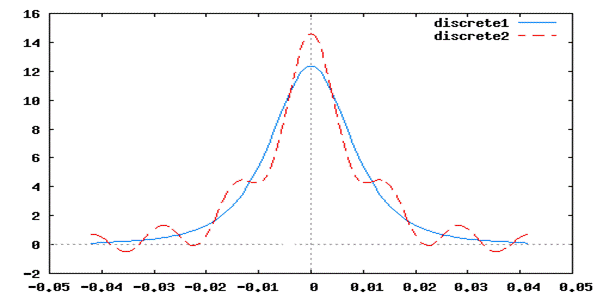
На этом рис. сплошной линией изображен нормированный на максимум восстановленный сигнал, а штриховой линией – исходный аналоговый сигнал. Очевидно, имеются существенные отличия в форме этих сигналов, что подтверждает вышесказанное, а именно то, что невозможно точно восстановить аналоговый сигнал по дискретному сигналу 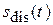, если интервал дискретизации 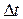сигнала превосходит максимально возможное значение, устанавливаемое теоремой Котельникова ().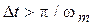

Однако из сравнения спектров исходного аналогового сигнала и дискретного сигнала с шагом дискретизации 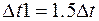следует, что эти спектры практически совпадают на интервале 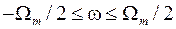. Следовательно, можно предложить следующий подход к восстановлению аналогового сигнала. Подадим такой дискретный сигнал на идеальный ФНЧ с частотой среза 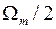. В результате получим, конечно, не абсолютно точно восстановленный сигнал. Однако его отличие от исходного аналогового сигнала будет уже не столь значительным, чем в предыдущем случае. Действительно, имеем

KF4(w):=(h(w+Wm/2)-h(w-Wm/2))$

SF_4(w):=SFDis1(w)*KF4(w)$

SF_4d:map(SF_4,wN3),numer$

asw4:makelist(realpart(sum(SF_4d[n] *exp(%i*tK[k]*wN3[n]),n,1,N)),k,1,K)$

wxplot2d([[discrete,tK,ass],[discrete,tK,asw4]]);

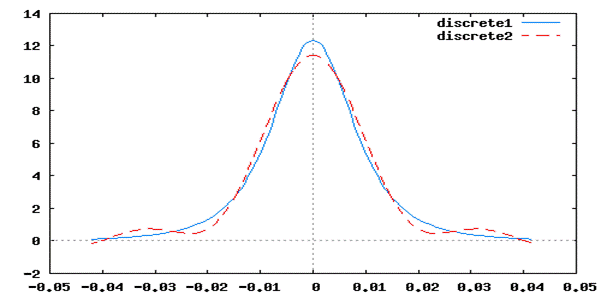
Сравнивая сплошные линии на двух последних рисунках, убеждаемся в том, что рассматриваемый подход к восстановлению сигнала более целесообразен.

Дата добавления: 2015-07-20