Пример выполнения задания 2. Рассмотрим в качестве детерминированного сигнала сигнал вида s(t)=1/(1+cosh(t/t0))

Рассмотрим в качестве детерминированного сигнала сигнал вида s(t) =1/(1+cosh(t/t0)). Причем параметр [сек] может принимать два значения: и . Зарисуем график этого сигнала для перечисленных значений параметра :

kill(all)$

numer:true$ ratprint:false$

t0L:[1d-3,0.5d-3]$

s(t,t0):=1/(1+cosh(t/t0))$

wxplot2d([s(t,t0L[1]),s(t,t0L[2])],[t,-0.01,0.01])$

Нетрудно заметить, что при уменьшении параметра длительность сигнала уменьшается.

Энергию сигнала будем вычислять следующим образом. Учтем, что сигнал имеет по оси времени бесконечную протяженность и, следовательно, осуществить вычисление энергии по формуле численными методами точно невозможно. Поэтому, учитывая четность и монотонный характер сигнала , находим такое значение момента времени T, при котором доля энергии сигнала на интервале 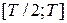составляет малую часть энергии сигнала, вычисленную на интервале . Набираем:

E1(t1,t2,t0):=2*quad_qag((s(x,t0))^2,x,t1,t2,0,'epsrel=1d-8)[1]$ TOL:1d-5$

T0(t0):=find_root(E1(TT/2,TT,t0)/E1(0,TT,t0)-TOL, TT, t0, 20*t0)$ T0m:map(T0,t0L),numer;

В результате получаем следующие значения моментов окончания сигнала для двух значений параметра :

[0.013301237077746,0.0066506185388731]

Следовательно, энергия сигнала для разных значений параметра определится как

[6.6666666665548874*10^-4,3.3333333332774437*10^-4]

Перейдем теперь к определению импульсной характеристики согласованного фильтра. В соответствии с формулой (7) импульсная характеристика согласованного фильтра определяется формой сигнала . Параметр в (7) обычно выбирают равным моменту окончания входного сигнала. В нашем случае параметр для двух значений определен выше. Константу c в (7) положим равной 1. Следовательно, импульсная характеристика согласованного фильтра определится оператором

h(t,TT0,t0):=s(TT0-t,t0),numer$

Тогда оператор вычисления детерминированной составляющей сигнала на выходе согласованного фильтра в соответствии с интегралом свертки запишется в виде

ys(t,TT0,t0):=quad_qag(s(x,t0)*h(t-x,TT0,t0),x, -TT0,t,0,'epsrel=1d-2)[1]$

Выводим на экран зависимости выходного сигнала от времени для двух значений параметра :

tL:makelist(k*5d-4,k,0,50)$

ys1:makelist(ys(tL[k],T0m[1],t0L[1]),k,1,51),numer$

ys2:makelist(ys(tL[k],T0m[2],t0L[2]),k,1,51),numer$

wxplot2d([[discrete,tL,ys1],[discrete,tL,ys2]], [y,0,0.001]);

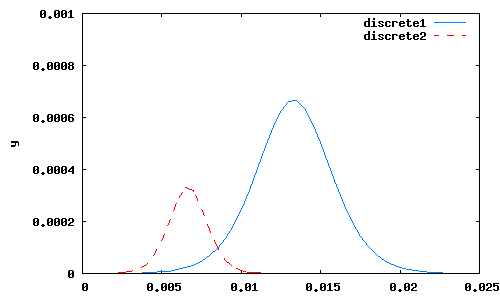
С помощью процедуры extremal_subset находим точки на графике, соответствующие максимальным значениям сигнала при заданных :

ysf1(t):=ys(t,T0m[1],t0L[1]),numer$

ysf2(t):=ys(t,T0m[2],t0L[2]),numer$

tLs:setify(tL)$

extremal_subset (tLs, ysf1, max),numer;

extremal_subset (tLs, ysf2, max),numer;

{0.0135}

{0.0065}

Сравнить координаты этих точек с величинами и (), рассчитанными ранее. Сделать соответствующие выводы.

Дата добавления: 2015-07-20