Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Характеристическим уравнением матрицы

Обратная матрица. | Система линейных уравнений. Определение совместной, не совместной системы | Матричный способ решения систем линейных уравнений. | Формулы Крамера. | Теорема Кронекера-Капелли. | Метод Гаусса. | Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними | Линейная зависимость и независимость системы векторов. Пусть имеется n векторов. | Теорема. (О разложении вектора по базису.) | Подпространство |


Читайте также:
  1. IPS-матрицы.
  2. MVA- матрицы.
  3. В) Построение прогнозирующей функции, описываемой уравнением гиперболы
  4. Вычисление определителя матрицы
  5. Квадратные матрицы. Обратная матрица.
  6. Матрицы
  7. Матрицы графов.

называется уравнение

 

Корни этого уравнения l1, l2, l3 называются характеристическими числами матрицы; они всегда вещественны, если исходная матрица была симметрической.
Система уравнений

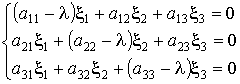
в которой l имеет одно из значений l1, l2, l3 и определитель которой в силу этого равен нулю, определяет тройку чисел (x1, x2, x3), соответствующую данному характеристическому числу.
Эта совокупность трех чисел (x1, x2, x3) определяет вектор r=1i+2j+3k, называемый собственным вектором матрицы.

 

 

Дата добавления: 2015-07-25; просмотров: 73 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Собственные числа и собственные вектора| Сказание о потопе
mybiblioteka.su - 2015-2024 год. (0.006 сек.)