Читайте также:
|
Пусть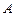 
– квадратная матрица порядка 
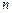и 
.
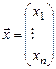Число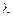 
называется собственным значением матрицы 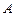, если существует ненулевой вектор 
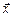, такой что выполнено равенство
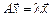(1)
Вектор 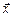, удовлетворяющий (1) называется собственным вектором матрицы 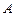, соответствующим собственному значению .
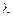Справедливы следующие свойства.
1. Собственному вектору матрицы соответствует единственное собственное значение.
Действительно, если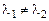 
– два собственных значения вектора 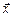, то 
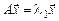и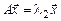 
, откуда 
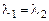или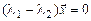 
, значит 
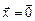, что противоречит определению. Значит .
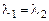2. Если 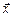собственный вектор матрицы 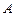, удовлетворяющий собственному значению 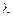, и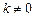 
– произвольное действительное число, то 
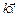- так же собственный вектор 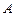с собственным значением .
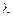Действительно, умножим обе части равенств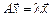а на 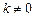, получим 
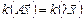или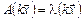 
, следовательно, ненулевой вектор 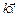, удовлетворяет определению и поэтому является собственным вектором матрицы 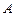, соответствующим собственному значению .
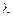3. Если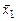 
и 
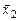линейно независимые собственные векторы матрицы 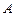с одним и тем же собственным значением 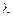, то 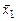+ 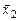– собственный вектор 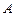с собственным значением .
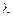Действительно, в силу линейной независимост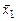и и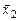 
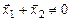, причём 
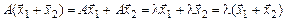, что согласно определению и означает, что вектор 
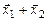– собственный, отвечающий собственному значению .
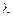4. Собственные векторы матрицы 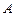, соответствующие попарно различным собственным значениям являются линейно независимыми.
Докажем свойство для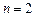 
. Пусть 
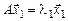и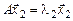 
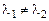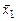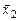, . Предположим, что и - линейно зависимы, следовательно, существует линейная комбинация 
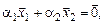причём хотя бы один из коэффициентов 
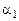и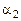 
ненулевой. Пусть 
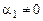, тогда 
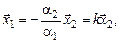где 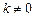. Значит, согласно свойству 2 вектор 
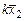является собственным вектором матрицы 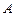, отвечающим собственному значению 
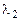. Из единственности собственного значения для вектора 
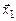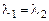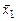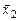следует, что . Значит, векторы и линейно независимы.
Вернёмся теперь к равенству (1) и преобразуем его.
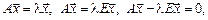получим
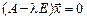(2)
В развёрнутом виде (2) есть однородная система уравнений с неизвестными. Такая система согласно следствию 2 из §15 имеет ненулевое решение тогда и только тогда, когда её определитель равен нулю, то есть
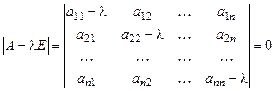(3)
по 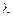. Он называется характеристическим многочленом матрицы 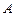. Уравнение (3) называется характеристическим уравнением, а его корни – характеристические числа или собственные значения матрицы 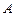. Совокупность всех собственных значений матрицы 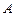с учётом их кратности (как корней характеристического уравнения) называется спектром матрицы .
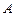Дата добавления: 2015-07-25; просмотров: 35 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Подпространство | | | Характеристическим уравнением матрицы |