
Читайте также:
|
Скласти рівняння лінії, для якої сума відстаней до точок
А(2;3) і В(4;5) дорівнює 54.
Розв’язання:
Візьмемо довільну точку лінії. М(х;у) 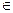 ГМТ. Згідно умові
ГМТ. Згідно умові  . Застосуємо формулу відстані між 2 точками:
. Застосуємо формулу відстані між 2 точками:
 , тоді у
, тоді у




 ,
,
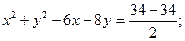

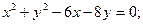
 .
.
Відповідь:  окружность R= 5; C(3;4)
окружность R= 5; C(3;4)
Контрольна робота №3.
Завдання 1.
Визначити ОДЗ функції: а)  .
.
Розв’язання:
ОДЗ: 
 , -5
, -5 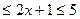 , - 6
, - 6  ,
, 
Відповідь: 
б)  ,
, 
 =
=  =
= 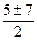 - 6, 1.
- 6, 1.
 та
та 
Відповідь: 
с) 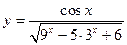 ,
, 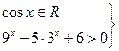
 ,
,  t1,2 =
t1,2 = 
 t1,2 = 2; 3
t1,2 = 2; 3
 або
або  , х = 1 або
, х = 1 або 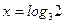
 та
та  .
.
Відповідь: 
Завдання 2.
Обчислити границі функції: 1)  , 2)
, 2) 
3) 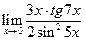 , 4)
, 4)  , 5)
, 5)  , 6)
, 6) 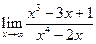
7) 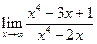 , 8)
, 8)  , 9)
, 9)  , 10)
, 10) 
Розв’язання:
1)  =
=  =
=  .
.
2)  =
=  =
=  =
=  =
= 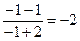 .
.
3) 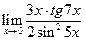 =
=  =
= 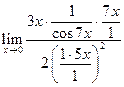 =
= 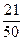 .
.
4)  =
=  =
=  =
=  =
=
= 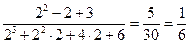 .
.
5)  =
=  =
=  .
.
6) 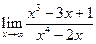 =
=  = 0.
= 0.
7) 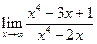 =
=  = 1.
= 1.
8)  =
= 

 =
= 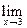

 =
=
= 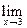

 =
= 
 .
.
9)  =
=  =
= 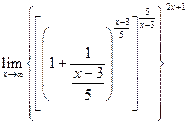 =
=  =
=  =
= 
10)  =
=  =
=  =
= 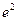
Завдання 3.
Визначити неперервність функції:
1.  в точках х = 1 та х = 2. 2)
в точках х = 1 та х = 2. 2) 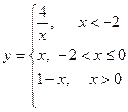
Розв’язання:
1. 
1) При х = 1:  функція визначена, оскільки існує границя
функція визначена, оскільки існує границя 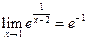 .
. 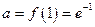 , тобто при х = 1 функція неперервна.
, тобто при х = 1 функція неперервна.
При х = 2:  функція невизначена, оскільки границя
функція невизначена, оскільки границя  .
.  ,
, 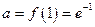 , тобто х = 2 точка розриву 2 роду.
, тобто х = 2 точка розриву 2 роду.
2. f(x) = 
 Розв’язання:
Розв’язання:
Перш за все, зробимо ескіз графіка функції.
 Функція визначена на всій числовій вісі, але із цього не випливає, що вона і неперервна тут, оскільки не елементарна (задана двома різними формулами на різних інтервалах змінення х). Функція може мати розрив в точці х = 0, де міняється її аналітичний вираз.
Функція визначена на всій числовій вісі, але із цього не випливає, що вона і неперервна тут, оскільки не елементарна (задана двома різними формулами на різних інтервалах змінення х). Функція може мати розрив в точці х = 0, де міняється її аналітичний вираз.
 Значення функції в точці х = 0:
Значення функції в точці х = 0:  .
.
Знайдемо односторонні границі:
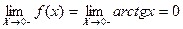 .
.
 .
.
Границі скінченні, але різні, тому
в точці х = 0 існує розрив І роду.
Стрибок функції:

В інших точках області визначення функція неперервна.
Відповідь: В х = 0 розриа 1 роду.
Перелік посилань (обов’язково) – не менш 5 джерел.
Дата добавления: 2015-07-25; просмотров: 32 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Завдання 2. | | | Додаток 3. |