Читайте также:
|
Розв’язати систему лінійних алгебраїчних рівнянь методом Гауса, за правилом Крамера, за допомогою оберненої матриці. Перевірити правильність обернення матриці та розв'язання системи.
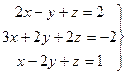Розв’язання:
1. Розв'яжемо систему методом Гаусса - метод послідовного виключення змінного. Для компактності запису скористаємося розширеною матрицею. Перетворимо її до діагонального виду.
= 
~ 
Отримаємо систему трикутного вигляду: 
, звідки:
(2; -1;-3)
2. Розв'яжемо систему методом Крамера – складемо і обчислимо 4 визначника:
Головний: 
, 
Допоміжні:
, 
, 
, 
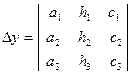
Відповідь: (2; - 1; -3)
3. Розв'яжемо систему за допомогою зворотньої матриці. Розв'яжемо матричне рівняння:
, 
, 
; 
; 
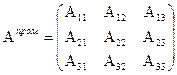, Апром. - проміжна матриця з алгебраїчних доповнень
елементів матриці системи 
, А* - транспонована матриця.
де 
- мінори.
; 
; 
;
. 
, 
, 
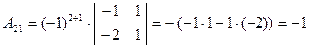
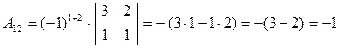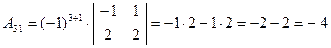
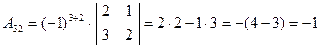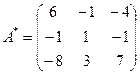- обернена матриця.
;
Перевірки:
1) Обертання матриці: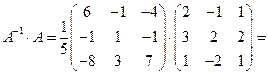 
= 
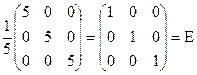
Отже, обернена матриця знайдена вірно.
2) 
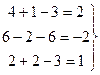
Тобто система розв’язана вірно.
Відповідь: 
Контрольна робота №2.
Завдання 1.
Знайти: 1) довжину ребра AB; Величини кутів:
2) між ребрами AB і AD,
3) між гранями ABC і ADC,
Дата добавления: 2015-07-25; просмотров: 32 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Завдання 9. | | | Побудувати піраміду у просторі ( x;y;z). |