Побудувати піраміду у просторі ( x;y;z).

Вершини піраміди відомі:

A (-2;0;-1)

B (0; 0; 4)

C (1; 3; 2)

D (3; 2; 7)

Розв’язання:

1)Довжину ребра знайдемо як відстань між двома точками:

,

= = , од.

2) Знайдемо напрямні вектори прямих, що містять ребра АВ, АС, АД

= (0 – (-2); 0 – 0; 4 – (-1)) = (2; 0; 5)

= (1 – (-2); 3 – 0; 2 – (-1)) = (3; 3; 3)

= (3 – (-2); 2 – 0; 7 – (-1)) = (5; 2; 8)

Кут між ребрами дорівнює куту між прямими, що утримують ці ребра, тобто між напрямними векторами цих прямих. Застосуємо скалярний добуток векторів:

3) Кут між гранями дорівнює куту між площинами, що утримують ці грані, тобто дорівнює куту між нормальними векторами цих площин.

Нехай Складемо рівняння цих граней (АВС):

5(х+2)+3у+2(Z+1), звідки

5х + 3у + 2Z – 8 = 0;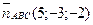

(АDС): = 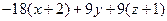, - 2х – 4 + у + Z + 1= 0; 2х – Z + 3 = 0

, ,

4)

,

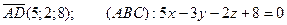
кут між ребром і гранню.

5) Грань піраміди представляє собою трикутник або половину паралелограму, побудованого на двох неколінеарних векторах. Площу знайдемо за допомогою векторного добутку цих векторів 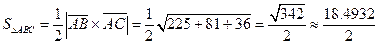≈ 9,5 од², оскільки

од²

6)Піраміда представляє собою шосту частину паралелепіпеда, побудованого на двох некомпланарних векторах. Застосуємо змішаний добуток цих векторів:

Vпір. 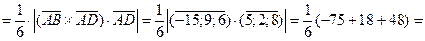од³

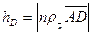7) . Довжина висоти: т. к. ,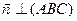

Перевірка:

7)Знайдемо координати проекції вершини D(3;2;7) на грань (АВС):

5х - 3у - 2Z + 8 = 0; Рівняння перпендикуляра :

;

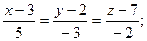
38 ; ; ;

.

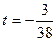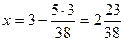9) Рівняння прямої, що проходе через вершину С(1;3;2) АD(5;2;8)

Пряма повинна мати той же нормальний вектор, що і задана пряма, тому .

10) Рівняння прямої, що проходе через вершину: В(0;0;4) площині (A;D;C): 2х-у- Z + 3 = 0; , оскільки нормаль площини є напрямляючим вектором прямої, яку шукаємо.

11) Рівняння прямої, що проходе через вершину: С(1;3;2) ребру , 2х + 5Z – 12 = 0.

12) Побудуємо піраміду по точкам.

A (-2;0;-1)

B (0; 0; 4)

C (1; 3; 2)

D (3; 2; 7)

Дата добавления: 2015-07-25